题目内容
 如图,AB为⊙O的弦,半径OC⊥AB于点D,AB=2
如图,AB为⊙O的弦,半径OC⊥AB于点D,AB=2| 3 |
考点:垂径定理,解直角三角形
专题:计算题
分析:连结OB,根据垂径定理得到AD=BD=
AB=
,再根据圆周角定理得∠COB=2∠A=60°,则可根据含30度的直角三角形三边的关系得到OD=
BD=1,OB=2OD=2,于是得到⊙O的直径为4.
| 1 |
| 2 |
| 3 |
| ||
| 3 |
解答: 解:连结OB,如图,
解:连结OB,如图,
∵半径OC⊥AB于点D,
∴AD=BD=
AB=
,
∵∠A=30°,
∴∠COB=2∠A=60°,
∴OD=
BD=1,
∴OB=2OD=2,
∴⊙O的直径为4.
故答案为4.
 解:连结OB,如图,
解:连结OB,如图,∵半径OC⊥AB于点D,
∴AD=BD=
| 1 |
| 2 |
| 3 |
∵∠A=30°,
∴∠COB=2∠A=60°,
∴OD=
| ||
| 3 |
∴OB=2OD=2,
∴⊙O的直径为4.
故答案为4.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
 如图,AB是半圆的直径,点D是弧AC的中点,∠B=50°,则下列判断不正确的是( )
如图,AB是半圆的直径,点D是弧AC的中点,∠B=50°,则下列判断不正确的是( )| A、∠ACB=90° |
| B、AC=2CD |
| C、∠DAB=65° |
| D、∠DAB+∠DCB=180° |
 如图,在一个边长为9cm的正方形ABCD中,点E、M分别是线段AC、CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于点H,交AD于点N.设点M从点C出发,以1cm/s的速度沿CD向点D运动;点E同时从点A出发,以
如图,在一个边长为9cm的正方形ABCD中,点E、M分别是线段AC、CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于点H,交AD于点N.设点M从点C出发,以1cm/s的速度沿CD向点D运动;点E同时从点A出发,以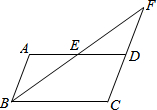 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是