题目内容
4.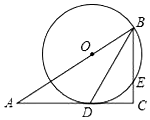 如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求CE的长.
分析 (1)连接OD,由BD为角平分线得到一对角相等,再根据等腰三角形的性质得出一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODA为直角,即可得证;
(2)过O作OG垂直于BE,可得出四边形ODCG为矩形,利用勾股定理求出BG的长,由垂径定理可得BE=2BG,中由切割线定理求出CE的长即可.
解答 (1)证明:连接OD,如图,
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,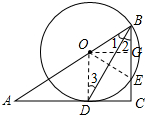
∴∠ODA=90°,
∴AC是⊙O的切线;
(2)解:过O作OG⊥BC,连接OE,
则四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BE,OB=OE,
∴BE=2BG=12.
解得:BE=12,
∵AC是⊙O的切线,
∴CD2=CE•CB,
即82=CE(CE+12),
解得:CE=4或CE=-16(舍去),
即CE的长为4.
点评 此题考查了切线的判定,等腰三角形的性质,矩形的判定与性质,平行线的判定与性质,切割线定理等知识;熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.化简$\frac{{a-{a^2}b}}{{a-{b^{-1}}}}$结果是( )
| A. | -ab | B. | ab-1 | C. | ab | D. | ab3 |
19.把一张圆形纸片按如图方式折叠两次后展开,图中的虚线表示折痕,则∠BOC的度数是( )


| A. | 120° | B. | 135° | C. | 150° | D. | 165° |
9.抛物线y=x2+mx+1的顶点在坐标轴上,则m的值( )
| A. | 0 | B. | -2 | C. | ±2 | D. | 0,±2 |
2. 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OBA的度数( )
如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OBA的度数( )
 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OBA的度数( )
如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OBA的度数( )| A. | 25° | B. | 50° | C. | 60° | D. | 30° |
 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为20米(如图所示),设这个苗圃园垂直于墙的一边长为x米
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为20米(如图所示),设这个苗圃园垂直于墙的一边长为x米