题目内容
20.观察:(1)$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$;
(2)$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$;
(3)$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$;
…
则($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$)×2015的值是多少?
分析 由$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$;$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$;$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$…可以看出$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,由此方法拆分计算得出答案即可.
解答 解:$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$…,
($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$)×2015
=(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$)×2015
=(1-$\frac{1}{2015}$)×2015
=2014.
故答案为:$\frac{1}{3}$,$\frac{1}{4}$.
点评 此题考查数字的变化规律,找出数字的变化规律,得出运算的方法,由此解决问题.

练习册系列答案
相关题目
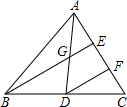 如图,AD是△ABC的中线,AE=EF=FC,则$\frac{AG}{AD}$=$\frac{1}{2}$,$\frac{GE}{BE}$=$\frac{1}{3}$.
如图,AD是△ABC的中线,AE=EF=FC,则$\frac{AG}{AD}$=$\frac{1}{2}$,$\frac{GE}{BE}$=$\frac{1}{3}$. 已知α,β为锐角,tanα=$\frac{1}{7}$,tanβ=2,利用如图所示的网格计算tan(α+β)的值为3.
已知α,β为锐角,tanα=$\frac{1}{7}$,tanβ=2,利用如图所示的网格计算tan(α+β)的值为3.