题目内容
10.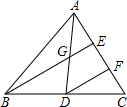 如图,AD是△ABC的中线,AE=EF=FC,则$\frac{AG}{AD}$=$\frac{1}{2}$,$\frac{GE}{BE}$=$\frac{1}{3}$.
如图,AD是△ABC的中线,AE=EF=FC,则$\frac{AG}{AD}$=$\frac{1}{2}$,$\frac{GE}{BE}$=$\frac{1}{3}$.
分析 根据三角形中位线定理得到AG=GD,求出$\frac{AG}{AD}$;根据三角形中位线定理得到GE=$\frac{1}{2}$DF,DF=$\frac{1}{2}$BE,得到答案.
解答 解:∵AD是△ABC的中线,EF=FC,
∴DF∥BE,又AE=EF,
∴AG=GD,
∴$\frac{AG}{AD}$=$\frac{1}{2}$,
∵AE=EF,AG=GD,
∴GE=$\frac{1}{2}$DF,
∵AD是△ABC的中线,EF=FC,
∴DF=$\frac{1}{2}$BE,
∴$\frac{GE}{BE}$=$\frac{1}{3}$,
故答案为:$\frac{1}{2}$;$\frac{1}{3}$.
点评 本题考查的是平行线分线段成比例定理、三角形中位线定理,掌握三角形的中位线平行于第三边并且等于第三边的一半是解题的关键,

练习册系列答案
相关题目
2.在测量旗杆的方案中,若旗杆高为21m,目测点到杆的距离为15m,则目测点到杆顶的距离为(设目高为1m)( )
| A. | 20m | B. | 25m | C. | 30m | D. | 35m |
 已知:如图,∠A=∠D=90°,AB=CD,AC与BD相交于点F,E是BC的中点.求证:∠BFE=∠CFE.
已知:如图,∠A=∠D=90°,AB=CD,AC与BD相交于点F,E是BC的中点.求证:∠BFE=∠CFE.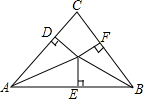 如图,OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,且OD=OE=OF,若∠C=80°,则∠AOB=130°.
如图,OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,且OD=OE=OF,若∠C=80°,则∠AOB=130°.