题目内容
9.已知关于x的一元二次方程x2-(k+2)x+(2k-1)=0.(1)求证:该方程由两个不相等的实数根.
(2)若此方程有一个根是1,请求出方程的另一个根,并求出以此两根为边长的等腰三角形的周长.
分析 (1)要证明方程有两个不相等的实数根,即证明△>0即可.△=[-(k+2)]2-4(2k-1)=k2-6k+13=(k-2)2+4,因为(k-2)2≥0,可以得到△>0;
(2)将x=1代入方程x2-(k+1)x+2k-3=0,求出k的值,进而得出方程的解,探讨得出等腰三角形的周长.
解答 (1)证明:∵△=[-(k+2)]2-4(2k-1)=k2-4k+8=(k-2)2+4,
而(k-2)2≥0,
∴△>0.
∴对任意实数k,方程有两个不相等的实数根;
(2)解:∵方程的一个根是1,
∴12-(k+2)+2k-1=0,
解得:k=2,
∴原方程为:x2-4x+3=0,
解得:x1=1,x2=3.
方程的另一个根是3,
等腰三角形的三边长为3,3,1,周长为3+3+1=7.
点评 此题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.同时考查了一元二次方程的解的定义.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | -(x+1)=-x-1 | B. | -(x+1)=-x+1 | C. | -(x+1)=x+1 | D. | -(x+1)=x-1 |
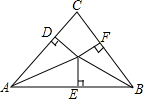 如图,OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,且OD=OE=OF,若∠C=80°,则∠AOB=130°.
如图,OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,且OD=OE=OF,若∠C=80°,则∠AOB=130°.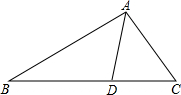 如图,在△ABC中,AD平分∠BAC,∠C=2∠B,试判断AB,AC,CD三者之间的数量关系,并说明理由.(想一想,你会几种方法)
如图,在△ABC中,AD平分∠BAC,∠C=2∠B,试判断AB,AC,CD三者之间的数量关系,并说明理由.(想一想,你会几种方法)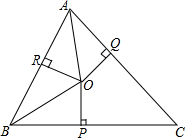 如图,已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
如图,已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.