题目内容
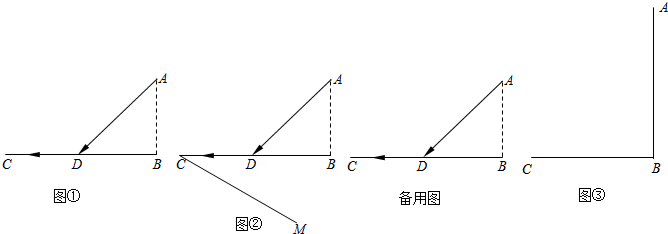
已知直线l1∥l2,直线l3与l1、l2分别交于C、D两点,点P是直线l3上的一动点
(1)如图,若动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中是否始终具有∠3+∠1=∠2这一相等关系?试说明理由;
(2)如图,当动点P在线段CD之外且在的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
(3)请画出动点P在线段CD之外且在直线的下方运动(不与C、D两点重合)时的图形,并仿照图①、图②标出∠1,∠2,∠3,此时∠1,∠2,∠3之间有何等量关系,请直接写出结论,不必说明理由.

(1)如图,若动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中是否始终具有∠3+∠1=∠2这一相等关系?试说明理由;
(2)如图,当动点P在线段CD之外且在的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
(3)请画出动点P在线段CD之外且在直线的下方运动(不与C、D两点重合)时的图形,并仿照图①、图②标出∠1,∠2,∠3,此时∠1,∠2,∠3之间有何等量关系,请直接写出结论,不必说明理由.

考点:平行线的性质
专题:计算题
分析:(1)∠3+∠1=∠2成立,理由如下:过点P作PE∥l1,利用两直线平行内错角相等得到∠1=∠AEP,根据l1∥l2,得到PE∥l2,再利用两直线平行内错角相等,根据∠BPE+∠APE=∠2,等量代换即可得证;
(2)∠3+∠1=∠2不成立,新的结论为∠3-∠1=∠2,理由为:过P作PE∥l1,同理得到∠3=∠BPE,根据∠BPE-∠APE=∠2,等量代换即可得证.
(2)∠3+∠1=∠2不成立,新的结论为∠3-∠1=∠2,理由为:过P作PE∥l1,同理得到∠3=∠BPE,根据∠BPE-∠APE=∠2,等量代换即可得证.
解答: 解:(1)∠3+∠1=∠2成立,理由如下:
解:(1)∠3+∠1=∠2成立,理由如下:
过点P作PE∥l1,
∴∠1=∠AEP,
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE,
∵∠BPE+∠APE=∠2,
∴∠3+∠1=∠2;
(2)∠3+∠1=∠2不成立,新的结论为∠3-∠1=∠2,理由为:
过P作PE∥l1,
∴∠1=∠APE,
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE,
∵∠BPE-∠APE=∠2,
∴∠3-∠1=∠2.
 解:(1)∠3+∠1=∠2成立,理由如下:
解:(1)∠3+∠1=∠2成立,理由如下:过点P作PE∥l1,
∴∠1=∠AEP,
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE,
∵∠BPE+∠APE=∠2,
∴∠3+∠1=∠2;
(2)∠3+∠1=∠2不成立,新的结论为∠3-∠1=∠2,理由为:
过P作PE∥l1,
∴∠1=∠APE,
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE,
∵∠BPE-∠APE=∠2,
∴∠3-∠1=∠2.
点评:此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
下列说法正确的是( )
| A、对角线相等的四边形是平行四边形 |
| B、对角线互相平分且垂直的四边形是矩形 |
| C、对角线平分相等且垂直的四边形是正方形 |
| D、对角线平分且相等的四边形是菱形 |
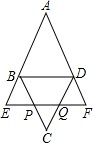 如图,在?ABCD中,点E、F分别在AB、AD延长线上,使得EF∥BD,连接EF,分别交BC、CD于点P、Q,已知BE=BP.求证:
如图,在?ABCD中,点E、F分别在AB、AD延长线上,使得EF∥BD,连接EF,分别交BC、CD于点P、Q,已知BE=BP.求证:
 如图,在边长为a的正方形ABCD中,点 G、M分别为AD、AB的中点,MN⊥MD,BN平分∠CBE并交MN于N.
如图,在边长为a的正方形ABCD中,点 G、M分别为AD、AB的中点,MN⊥MD,BN平分∠CBE并交MN于N.