题目内容
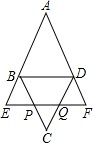 如图,在?ABCD中,点E、F分别在AB、AD延长线上,使得EF∥BD,连接EF,分别交BC、CD于点P、Q,已知BE=BP.求证:
如图,在?ABCD中,点E、F分别在AB、AD延长线上,使得EF∥BD,连接EF,分别交BC、CD于点P、Q,已知BE=BP.求证:(1)∠E=∠F;
(2)?ABCD是菱形.
考点:菱形的判定,平行四边形的性质
专题:
分析:(1)根据等腰三角形性质得出∠E=∠BPE,根据平行四边形性质得出BC∥AD,推出∠BPE=∠F,即可得出答案;
(2)求出∠BPE=∠DQF,根据平行线性质得出∠CBD=∠BPE,∠BDC=∠DQF,推出∠CBD=∠CDB,推出BC=DC,根据菱形的判定推出即可.
(2)求出∠BPE=∠DQF,根据平行线性质得出∠CBD=∠BPE,∠BDC=∠DQF,推出∠CBD=∠CDB,推出BC=DC,根据菱形的判定推出即可.
解答:证明:(1)∵BE=BP,
∴∠E=∠BPE,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠BPE=∠F,
∴∠E=∠F;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DQF=∠E,
∵∠E=∠F,∠BPE=∠E,
∴∠BPE=∠DQF,
∵EF∥BD,
∴∠CBD=∠BPE,∠BDC=∠DQF,
∴∠CBD=∠CDB,
∴BC=DC,
∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形.
∴∠E=∠BPE,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠BPE=∠F,
∴∠E=∠F;

(2)∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DQF=∠E,
∵∠E=∠F,∠BPE=∠E,
∴∠BPE=∠DQF,
∵EF∥BD,
∴∠CBD=∠BPE,∠BDC=∠DQF,
∴∠CBD=∠CDB,
∴BC=DC,
∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形.
点评:本题考查了平行四边形的性质,菱形的判定,平行线的性质,等腰三角形的性质和判定的应用,注意:菱形的判定定理有:①有一组邻边相等的平行四边形是菱形,②四条边都相等的四边形是菱形,③对角线互相垂直的平行四边形是菱形.

练习册系列答案
相关题目
已知一个n边形减去一个角后,其余(n-1)个角的和是1150°,则减去的这个内角的度数与n的值分别为( )
| A、70°,7 |
| B、110°,7 |
| C、110°,9 |
| D、70°,9 |
若关于x的不等式(a+1)x>2a+2的解集是x<2,则a的取值范围为( )
| A、a>0 | B、a<0 |
| C、a>-1 | D、a<-1 |

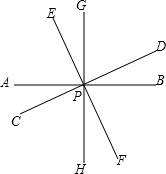 如图,直线AB、CD、EF和GH相交于点P,且∠APC=25°,∠EPG=25°,∠BPF=65°,问哪些直线互相垂直?为什么?
如图,直线AB、CD、EF和GH相交于点P,且∠APC=25°,∠EPG=25°,∠BPF=65°,问哪些直线互相垂直?为什么?