题目内容
 如图,在边长为a的正方形ABCD中,点 G、M分别为AD、AB的中点,MN⊥MD,BN平分∠CBE并交MN于N.
如图,在边长为a的正方形ABCD中,点 G、M分别为AD、AB的中点,MN⊥MD,BN平分∠CBE并交MN于N.(1)证明:∠ADM=∠NMB;
(2)证明:△DGM≌△MBN;
(3)求△DMN的面积.
考点:全等三角形的判定与性质,正方形的性质
专题:
分析:(1)通过角的计算由∠ADM+∠DMG=45°,∠DMG+∠NMB=135°-90°=45°得出∠ADM=∠NMB.
(2)求出∠MBN=∠DGM,再运用ASA来求证△DGM≌△MBN.
(3)先运用勾股定理求出DM的长度,再运用△DGM≌△MBN知DM=MN求出△DMN的面积.
(2)求出∠MBN=∠DGM,再运用ASA来求证△DGM≌△MBN.
(3)先运用勾股定理求出DM的长度,再运用△DGM≌△MBN知DM=MN求出△DMN的面积.
解答:证明:(1)∵四边形ABCD是正方形,点 G、M分别为AD、AB的中点,
∴∠AGM=∠AMG=45°,
∴∠GMB=180°-∠AMG=135°,∠ADM+∠DMG=45°
又∵MN⊥MD
∴∠DMN=90°
∴∠DMG+∠NMB=135°-90°=45°
∴∠ADM+∠DMG=∠DMG+∠NMB
∴∠ADM=∠NMB
(2)∵BN平分∠CBE
∴∠CBN=∠NBE=45°
∴∠MBN=135°
又∵∠DGM=180°-45°=135°
∴∠MBN=∠DGM
∵四边形ABCD是正方形,点 G、M分别为AD、AB的中点,
∴DM=MB
由(1)得∴∠ADM=∠NMB
∴△DGM≌△MBN(ASA)
(3)∵RT△DAM中,AM=
a,AD=a
∴DM=
=
a
∵△DGM≌△MBN
∴MN=DM=
a
∴RT△DMNR的面积=
a×
a÷2=
a
∴∠AGM=∠AMG=45°,
∴∠GMB=180°-∠AMG=135°,∠ADM+∠DMG=45°
又∵MN⊥MD
∴∠DMN=90°
∴∠DMG+∠NMB=135°-90°=45°
∴∠ADM+∠DMG=∠DMG+∠NMB
∴∠ADM=∠NMB
(2)∵BN平分∠CBE
∴∠CBN=∠NBE=45°
∴∠MBN=135°
又∵∠DGM=180°-45°=135°
∴∠MBN=∠DGM
∵四边形ABCD是正方形,点 G、M分别为AD、AB的中点,
∴DM=MB
由(1)得∴∠ADM=∠NMB
∴△DGM≌△MBN(ASA)
(3)∵RT△DAM中,AM=
| 1 |
| 2 |
∴DM=
(
|
| ||
| 2 |
∵△DGM≌△MBN
∴MN=DM=
| ||
| 2 |
∴RT△DMNR的面积=
| ||
| 2 |
| ||
| 2 |
| 5 |
| 8 |
点评:考查了正方形的性质和全等三角形的知识,主要利用正方形的性质,全等三角形的性质与判定来解题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
若关于x的不等式(a+1)x>2a+2的解集是x<2,则a的取值范围为( )
| A、a>0 | B、a<0 |
| C、a>-1 | D、a<-1 |

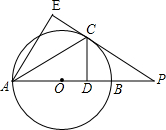 如图,⊙O中,AB是直径,AC是弦,CD⊥AB于D,将△ACD沿AC折叠得到△ACE,延长EC交AB的延长线于点P.
如图,⊙O中,AB是直径,AC是弦,CD⊥AB于D,将△ACD沿AC折叠得到△ACE,延长EC交AB的延长线于点P.