题目内容
平面上5条直线两两相交,任何三条直线不交于同一点,则一共形成 对同旁内角.
考点:同位角、内错角、同旁内角
专题:
分析:根据n条直线两两相交,共有
n(n-1)个点;任意两条直接被第三条截有2对同旁内角,再计算得出n条直线两两相交于不同点,同旁内角的对数.
| 1 |
| 2 |
解答:解:n条直线两两相交,共有
n(n-1)个点;任意两条直接被第三条截有2对同旁内角,首先n条里面取两条,剩下n-2条,得到
n(n-1)×4×(n-2)=2n(n-1)(n-2)对同旁内角,且又互相重复,所以可得n(n-1)(n-2)
所以把n=5代入得:n(n-1)(n-2)=5×(5-1)×(5-2)=60,
故答案为:60.
| 1 |
| 2 |
| 1 |
| 2 |
所以把n=5代入得:n(n-1)(n-2)=5×(5-1)×(5-2)=60,
故答案为:60.
点评:本题考查了同位角、内错角、同旁内角的定义.注意在截线的同旁找同位角,在被截直线之间找内错角、同旁内角.要结合图形,熟记同位角、内错角、同旁内角的位置特点.两条直线被第三条直线所截所形成的八个角中,有4组同位角.

练习册系列答案
相关题目
 如图,AD=2cm,AB=6cm,P点沿AB边从点A开始向B以2cm/秒移动,点Q沿DA边从点D开始向A以1cm/秒移动,移动t秒.
如图,AD=2cm,AB=6cm,P点沿AB边从点A开始向B以2cm/秒移动,点Q沿DA边从点D开始向A以1cm/秒移动,移动t秒.(1)当t为何值时,AP=
| 1 |
| 2 |
(2)当t为何值时,AQ=PC.
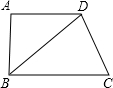 如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=BD.
如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=BD. △ABC中,∠A=42°,D、E为∠ABC与∠ACB三等分线的交点,则∠D=
△ABC中,∠A=42°,D、E为∠ABC与∠ACB三等分线的交点,则∠D= 在梯形ABCD中,AB∥DC,AB<DC,点P为BD中点,记S△APB=S1,S△PDC=S2,梯形ABCD的面积为S,下面四个结论:
在梯形ABCD中,AB∥DC,AB<DC,点P为BD中点,记S△APB=S1,S△PDC=S2,梯形ABCD的面积为S,下面四个结论: 已知点D是△ABC的边AB上的中点,点E是AC上的一点,DF∥BE,EF∥AB,证明:AE、DF互相平分.
已知点D是△ABC的边AB上的中点,点E是AC上的一点,DF∥BE,EF∥AB,证明:AE、DF互相平分. 如图,A、B、C、D是半径为10的⊙O上的四点,其中∠CAD=∠ABD°=60°.
如图,A、B、C、D是半径为10的⊙O上的四点,其中∠CAD=∠ABD°=60°. 如图,在△ABC中,∠B=90°,BC=20cm,AD是角平分线,且BD:CD=2:3,求点D到AC边上的距离.
如图,在△ABC中,∠B=90°,BC=20cm,AD是角平分线,且BD:CD=2:3,求点D到AC边上的距离.