题目内容
 如图,AD=2cm,AB=6cm,P点沿AB边从点A开始向B以2cm/秒移动,点Q沿DA边从点D开始向A以1cm/秒移动,移动t秒.
如图,AD=2cm,AB=6cm,P点沿AB边从点A开始向B以2cm/秒移动,点Q沿DA边从点D开始向A以1cm/秒移动,移动t秒.(1)当t为何值时,AP=
| 1 |
| 2 |
(2)当t为何值时,AQ=PC.
考点:一元一次方程的应用
专题:几何动点问题
分析:(1)根据题意表示出AQ与AP,代入AP=
AQ中,求出t的值即可;
(2)连接CP,利用勾股定理表示出CP,代入AQ=CP中计算即可.
| 1 |
| 2 |
(2)连接CP,利用勾股定理表示出CP,代入AQ=CP中计算即可.
解答:
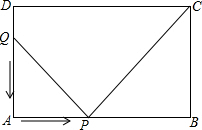 解:(1)根据题意得:AQ=(2-t)cm,AP=2tcm,
解:(1)根据题意得:AQ=(2-t)cm,AP=2tcm,
由AP=
AQ,得到2t=
(2-t),即4t=2-t,
解得:t=
,
则t=
秒时,AP=
AQ;
(2)连接PC,由AQ=PC,得到2-t=
,
整理得:3t2-20t+68=0,
∵△=400-4×3×68=-416<0,
∴方程无解,
则不存在t,使AQ=PC.
 解:(1)根据题意得:AQ=(2-t)cm,AP=2tcm,
解:(1)根据题意得:AQ=(2-t)cm,AP=2tcm,由AP=
| 1 |
| 2 |
| 1 |
| 2 |
解得:t=
| 2 |
| 5 |
则t=
| 2 |
| 5 |
| 1 |
| 2 |
(2)连接PC,由AQ=PC,得到2-t=
| (6-2t)2+62 |
整理得:3t2-20t+68=0,
∵△=400-4×3×68=-416<0,
∴方程无解,
则不存在t,使AQ=PC.
点评:此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
有理数-
的相反数是( )
| 1 |
| 2 |
| A、-2 | ||
B、
| ||
| C、2 | ||
D、-|-
|
 如图,将四棱锥沿某些棱剪开,展成一个平面图形,至少需要剪开( )
如图,将四棱锥沿某些棱剪开,展成一个平面图形,至少需要剪开( )| A、4条棱 | B、5条棱 |
| C、6条棱 | D、7条棱 |
下列命题中的假命题是( )
| A、圆心角的度数与它所对的弧的度数相等 |
| B、等弧所对的弦相等 |
| C、90°的圆周角所对的弦是直径 |
| D、三点确定一个圆 |
 如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )| A、AM=CN |
| B、AM∥CN |
| C、AB=CD |
| D、∠M=∠N |
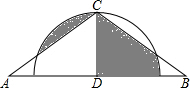 如图,在△ABC中,∠A=30°,AC=BC=12,过点C作CD⊥AB于D,以点D为圆心,CD为半径画半圆,则图中阴影部分的面积为
如图,在△ABC中,∠A=30°,AC=BC=12,过点C作CD⊥AB于D,以点D为圆心,CD为半径画半圆,则图中阴影部分的面积为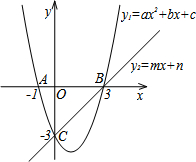 如图,在同一直角坐标系中,抛物线y1=ax2+bx+c与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),直线y2=mx+n与抛物线交于B、C两点.由图象可知:
如图,在同一直角坐标系中,抛物线y1=ax2+bx+c与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),直线y2=mx+n与抛物线交于B、C两点.由图象可知: