题目内容
 如图,在△ABC中,∠B=90°,BC=20cm,AD是角平分线,且BD:CD=2:3,求点D到AC边上的距离.
如图,在△ABC中,∠B=90°,BC=20cm,AD是角平分线,且BD:CD=2:3,求点D到AC边上的距离.考点:角平分线的性质
专题:
分析:过点D作DE⊥AC于点E,根据BC=20cm,BD:CD=2:3求出BD的长,再由角平分线的性质即可得出结论.
解答: 解:过点D作DE⊥AC于点E,
解:过点D作DE⊥AC于点E,
∵BC=20cm,BD:CD=2:3,
∴BD=
BC=8.
∵AD是角平分线,DB⊥AB,DE⊥AC,
∴DE=BD=8.
答:点D到AC边上的距离是8cm.
 解:过点D作DE⊥AC于点E,
解:过点D作DE⊥AC于点E,∵BC=20cm,BD:CD=2:3,
∴BD=
| 2 |
| 3 |
∵AD是角平分线,DB⊥AB,DE⊥AC,
∴DE=BD=8.
答:点D到AC边上的距离是8cm.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
下列图形中,绕某个点旋转180°后能与自身重合的有( )
①矩形;②等边三角形;③线段;④平行四边形.
①矩形;②等边三角形;③线段;④平行四边形.
| A、4个 | B、3个 | C、2个 | D、1个 |
下列图形中,不是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
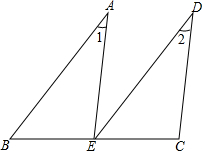 完成下面的说理过程,并在括号内填写理由.
完成下面的说理过程,并在括号内填写理由. 用8个相同的小正方形搭成一个几何体,其俯视图如图所示,那么这个几何体的左视图一定不是( )
用8个相同的小正方形搭成一个几何体,其俯视图如图所示,那么这个几何体的左视图一定不是( )