题目内容
 在梯形ABCD中,AB∥DC,AB<DC,点P为BD中点,记S△APB=S1,S△PDC=S2,梯形ABCD的面积为S,下面四个结论:
在梯形ABCD中,AB∥DC,AB<DC,点P为BD中点,记S△APB=S1,S△PDC=S2,梯形ABCD的面积为S,下面四个结论:(1)2(S1+S2)>S;(2)2(S1+S2)<S;(3)2(S1+S2)=S;(4)S1>S2;
其中,正确的是( )
| A、(1) | B、(2) |
| C、(3) | D、(4) |
考点:梯形
专题:
分析:利用三角形中线平分三角形面积进而求出即可.
解答:解:∵点P为BD中点,记S△APB=S1,S△PDC=S2,
∴S1=
S△ABD,S2=
S△BDC,
∴S1+S2=
S△ABD+
S△BDC=
S,
故2(S1+S2)=S.
故选:C.
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
∴S1+S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故2(S1+S2)=S.
故选:C.
点评:此题主要考查了梯形以及三角形中线的性质,得出S1=
S△ABD,S2=
S△BDC是解题关键.
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
 实数a、b在数轴上的位置如图所示,则下列结果正确的是( )
实数a、b在数轴上的位置如图所示,则下列结果正确的是( )| A、a>0 | B、ab>0 |
| C、a-b>0 | D、a+b>0 |
一个锐角是38度,它的余角的度数是( )
| A、38° | B、52° |
| C、142° | D、62° |
下列图形中,不是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
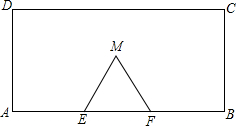 如图:在矩形ABCD中,AD=60cm,CD=120cm,E、F为AB边的三等分点,以EF为边在矩形内作等边三角形MEF,N为AB边上一点,EN=10cm;
如图:在矩形ABCD中,AD=60cm,CD=120cm,E、F为AB边的三等分点,以EF为边在矩形内作等边三角形MEF,N为AB边上一点,EN=10cm; 如图所示,OC平分∠AOB,OD平分∠AOC,且∠COD=23°,求∠AOB的度数.
如图所示,OC平分∠AOB,OD平分∠AOC,且∠COD=23°,求∠AOB的度数.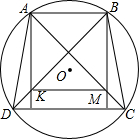 已知ABCD是圆的内接四边形,且AC⊥BD于P,由顶点A和B向CD引垂线分别交对角线BD、AC于K、M(如图),则四边形AKMB是菱形.
已知ABCD是圆的内接四边形,且AC⊥BD于P,由顶点A和B向CD引垂线分别交对角线BD、AC于K、M(如图),则四边形AKMB是菱形.