题目内容
3.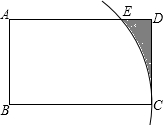 如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交边AD于点E,AB=4,BC=8,则图中弧$\widehat{CE}$,线段DE,CD围成的阴影部分的面积为32-8$\sqrt{3}$-$\frac{4π}{3}$.
如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交边AD于点E,AB=4,BC=8,则图中弧$\widehat{CE}$,线段DE,CD围成的阴影部分的面积为32-8$\sqrt{3}$-$\frac{4π}{3}$.
分析 连接BE.则阴影部分的面积等于矩形的面积减去直角三角形ABE的面积和扇形BCE的面积,根据题意,知BE=BC=8,则AE=4$\sqrt{3}$,∠ABE=60°,则∠CBE=30°进而求出即可.
解答 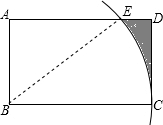 解:连接BE.
解:连接BE.
根据题意,知BE=BC=8.
则根据勾股定理,得AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=4$\sqrt{3}$,
∵cos∠BAE=$\frac{AB}{BE}$=$\frac{1}{2}$,
则∠ABE=60°.
则∠CBE=30°.
则阴影部分的面积=S四边形ABCD-S△ABE-S扇形DAE=4×8-$\frac{1}{2}$×4×4$\sqrt{3}$-$\frac{30π×{8}^{2}}{360}$=32-8$\sqrt{3}$-$\frac{4π}{3}$;
故答案为:32-8$\sqrt{3}$-$\frac{4π}{3}$.
点评 此题主要考查了扇形面积求法,本题中能够将不规则图形的面积进行转换成规则图形的面积差是解题的关键.

练习册系列答案
相关题目
 如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想:
如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想: 如图,在平行四边形ABCD中,E为BF延长线上一点,求证:$\frac{BO}{FO}$=$\frac{EO}{BO}$.
如图,在平行四边形ABCD中,E为BF延长线上一点,求证:$\frac{BO}{FO}$=$\frac{EO}{BO}$.
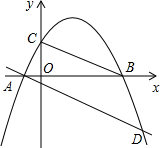 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B,与y轴交于点C,将直线BC平移,使其经过点A,且与抛物线交于点D,求证:∠BDA=45°.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B,与y轴交于点C,将直线BC平移,使其经过点A,且与抛物线交于点D,求证:∠BDA=45°.
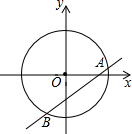 如图,在坐标系中以原点为圆心,半径为2的圆,直线y=kx-(k+1)与⊙O有两个交点A、B,则AB的最短长度是2$\sqrt{2}$.
如图,在坐标系中以原点为圆心,半径为2的圆,直线y=kx-(k+1)与⊙O有两个交点A、B,则AB的最短长度是2$\sqrt{2}$.