题目内容
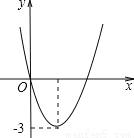
二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）
A. -3 B. 3 C. -6 D. 9
B
【解析】先根据抛物线的开口向上可知a＞0，由顶点纵坐标为-3得出b与a关系，再根据一元二次方程ax2+bx+m=0有实数根可得到关于m的不等式，求出m的取值范围即可．
【解析】
∵抛物线的开口向上，顶点纵坐标为-3，
∴a＞0， =-3，即b2=12a，
∵一元二次方程ax2+bx+m=0有实数根，
∴△=b2-4am≥0，即12a-4am≥0，即12-4m≥0，解得m≤3...
下列图形中不是轴对称而是中心对称图形的是（ ）
A. 等边三角形
B. 平行四边形
C. 矩形
D. 菱形
B
【解析】试题解析：等边三角形不是中心对称图形，对称轴为三条中线所在直线；平行四边形的对称中心为两条对角线的交点，不是轴对称图形；矩形的对称中心为两条对角线的交点，对称轴为两对边中点连线所在直线；菱形的对称中心为两条对角线的交点，对称轴为两条对角线所在直线；所以选择B． 如图，直线l1在平面直角坐标系中，直线l1与y轴交于点A，点B(－3,3)也在直线l1上，将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，点C恰好也在直线l1上．
(1)求点C的坐标和直线l1的解析式；
(2)若将点C先向左平移3个单位长度，再向上平移6个单位长度得到点D，请你判断点D是否在直线l1上；
(3)已知直线l2：y＝x＋b经过点B，与y轴交于点E，求△ABE的面积．
(1) C的坐标为(－2,1)，直线l1的解析式为y＝－2x－3；(2)点D在直线l1上；(3)△ABE的面积为13.5.
【解析】试题分析：（1）∵B（﹣3，3），将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，
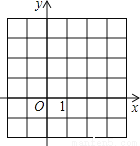
∴﹣3+1=﹣2，3﹣2=1，∴C的坐标为（﹣2，1），设直线l1的解析式为y=kx+c，∵点B、C在直线l1上，∴代入得：，解得：k=﹣2，c=﹣3，∴直线... （1）请在坐标系中画出二次函数y=x2﹣2x的大致图象；
（2）根据方程的根与函数图象的关系，将方程x2﹣2x=1的根在图上近似的表示出来（描点）；
（3）观察图象，直接写出方程x2﹣2x=1的根．（精确到0.1）
【解析】
（1）如下图，
y=x2﹣2x=（x﹣1） 2﹣1，
作出顶点，作出与x轴的交点，图象光滑．
（2）正确作出点M，N；
（3）写出方程的根为﹣0.4，2.4．
【解析】
（1）确定顶点坐标和与x轴y轴交点，作出图形；
（2）方程x2﹣2x=1的根就是二次函数y=x2﹣2x的函数值为1时的横坐标x的值；
（3）观察图象可知图象交点的横坐标即... 下列哪一个函数，其图象与x轴有两个交点（ ）
A. y=(x-23)2+155 B. y=(x+23)2+155
C. y= -(x-23)2-155 D. y= -(x+23)2+155
D
【解析】A、令y=0得，(x-23)2+155=0，移项得，(x-23)2= -155，方程无实根；
B、令y=0得，(x+23)2+155=0，移项得，(x+23)2= -155，方程无实根；
C、令y=0得，-(x-23)2-155=0，移项得，(x-23)2= -155，方程无实根；
D、令y=0得，-(x+23)2+155=0，移项得，(x+23)2=155，方... 如图，已知抛物线与x轴的一个交点A（1，0），对称轴是x= -1，则该抛物线与x轴的另一交点坐标是（ ）
A. （-3，0） B. （-2，0） C. x= -3 D. x= -2
A
【解析】抛物线与x轴的另一交点为B(b，0)，
∵抛物线与x轴的一个交点A(1，0)，对称轴是x＝－1，∴＝－1，
解得b＝－3，∴B(－3，0)． 若x2+2（m﹣1）x+36是完全平方式，则m=__．
7或﹣5
【解析】∵x2+2（m﹣1）x+36是完全平方式，
∴2（m﹣1）x=±2×6x,
∴m﹣1=±6,
∴m=7或m=-5. 如图1，在一条河同一岸边有A和B两个村庄，要在河边修建码头M，使M到A和B的距离之和最短，试确定M的位置；
见解析
【解析】试题分析：利用轴对称，作点A关于直线l的对称点A′，连接A′B交直线l于点M，则点M即为所求点.
试题解析：所求点如下图所示：
∵两点之间线段最短，
∴需要能将AM、BM两边转化到一条直线上，
∴用轴对称可以办到，
求点M的位置的具体步骤如下：
①作作点A关于直线BC的轴对称点A’，
②连结A’B交BC于点M，
③连结AM，
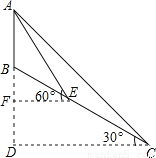
... 如图，小山顶上有一信号塔AB，山坡BC的倾角为30°，现为了测量塔高AB，测量人员选择山脚C处为一测量点，测得塔顶仰角为45°，然后顺山坡向上行走100米到达E处，再测得塔顶仰角为60°，求塔高AB.（结果保留整数
）
塔高AB大约为58米
【解析】【解析】
依题意可得：∠AEB=30°，∠ACE=15°，
又∵∠AEB=∠ACE+∠CAE，∴∠CAE=15°。
∴△ACE为等腰三角形。∴AE=CE=100米。
在Rt△AEF中，∠AEF=60°，∴EF=AEcos60°=50（米），AF=AEsin60°=50（米）。
在Rt△BEF中，∠BEF=30°，∴BF=EFtan30°...