题目内容
11.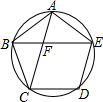 如图所示,正五边形ABCDE的对角线AC和BE相交于点F,求证:AC=AB+BF.
如图所示,正五边形ABCDE的对角线AC和BE相交于点F,求证:AC=AB+BF.
分析 运用圆周角定理,∠ABE=∠BAC,∠CBE=72°,即可根据等角对等边证明AF=BF,BC=CF,即可解决问题.
解答 解:∵⊙O是正五边形ABCDE的外接圆,
∴∠CBE=$\frac{1}{2}$×$\frac{2}{5}$×360°=72°.
∵⊙O是正五边形ABCDE的外接圆,
∴∠BAC=∠ABE=$\frac{1}{2}$×$\frac{1}{5}$×360°=36°,
∴AF=BF,
∠BFC=∠ABE+∠BAC=72°,
∴∠CBE=∠BFC,
∴BC=CF;
同理可证:∠PBC=∠PCB=36°,
∴AC=AF+CF=AB+BF.
点评 该题主要考查了正多边形和圆的关系及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
16.某电信公司给顾客提供了A、B、C三种宽带上网的收费方式:
设某用户每月的上网时间为x(小时),A、B、C三种收费方式的收费金额分别为y1、y2、y3(元).
(1)分别求y1、y1、y2关于x的函数关系式,并写出相应的自变量的取值范围;
(2)请你帮该用户选择较省钱的收费方式,并说明理由.
| 收费方式 | 月使用费/元 | 包时上网时间/小时 | 超时费/(元/分钟) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
(1)分别求y1、y1、y2关于x的函数关系式,并写出相应的自变量的取值范围;
(2)请你帮该用户选择较省钱的收费方式,并说明理由.
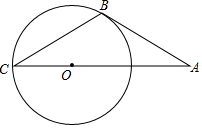 如图,直线AB是⊙O的切线,B为切点,AO的延长线交⊙O于点C,且∠A=30°,试判断AB与BC的大小关系.
如图,直线AB是⊙O的切线,B为切点,AO的延长线交⊙O于点C,且∠A=30°,试判断AB与BC的大小关系. 如图所示,有一根直立标杆,它的上部被风从B处吹折,杆顶C着地离杆底2米,修好后又被风吹折,因新断处D比前一次低0.5米,故杆顶E着地比前一次远1米,求原标杆的长度?
如图所示,有一根直立标杆,它的上部被风从B处吹折,杆顶C着地离杆底2米,修好后又被风吹折,因新断处D比前一次低0.5米,故杆顶E着地比前一次远1米,求原标杆的长度? 如图,△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若EF=5,则CE2+CF2=25.
如图,△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若EF=5,则CE2+CF2=25.