题目内容
12. 如图,在△ABC中,∠B>∠C,AE、AD分别是∠A的平分线和BC边上的高.求证:∠DAE=$\frac{1}{2}$(∠B-∠C).
如图,在△ABC中,∠B>∠C,AE、AD分别是∠A的平分线和BC边上的高.求证:∠DAE=$\frac{1}{2}$(∠B-∠C).
分析 根据三角形内角和定理以及AD是BC边上的高,求得∠BAD=90°-∠B,再根据AE平分∠BAC,求得∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C,最后根据∠DAE=∠BAE-∠BAD即可求解.
解答 证明:∵AD是BC边上的高,
∴∠BAD=90°-∠B.
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C.
∵∠DAE=∠BAE-∠BAD,
∴∠DAE=(90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C)-(90°-∠B)=$\frac{1}{2}$∠B-$\frac{1}{2}$∠C=$\frac{1}{2}$(∠B-∠C).
点评 本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是三角形的内角和定理:三角形内角和是180°.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
4.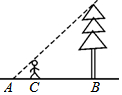 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )| A. | 4.8 m | B. | 6.4 m | C. | 8 m | D. | 10 m |
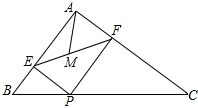 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为$\frac{6}{5}$.
如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为$\frac{6}{5}$. 如图,你能数出多少个不同的四边形?
如图,你能数出多少个不同的四边形?