题目内容
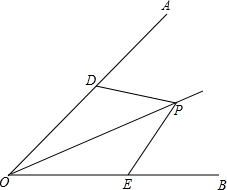 (1)如图,P为∠AOB的平分线上一点,点D、E分别在边OA、OB上.若∠PDO=∠PEO,则是否有PD=PE?为什么?
(1)如图,P为∠AOB的平分线上一点,点D、E分别在边OA、OB上.若∠PDO=∠PEO,则是否有PD=PE?为什么?(2)如图,点D、E分别在∠AOB的边OA、OB上,点P在∠AOB内部,∠PDO=∠PEO,且PD=PE,则点P在∠AOB的平分线上吗?为什么?
考点:全等三角形的判定与性质
专题:
分析:(1)根据AAS推出△DOP≌△EOP,根据全等三角形的性质得出即可;
(2)过P作PM⊥OA于M,PN⊥OB于N,求出∠PMD=∠PNE=90°,∠MDP=∠NEP,证出△PMD≌△PNE即可.
(2)过P作PM⊥OA于M,PN⊥OB于N,求出∠PMD=∠PNE=90°,∠MDP=∠NEP,证出△PMD≌△PNE即可.
解答:(1)解:PD=PE,
理由是:∵P为∠AOB的平分线上一点,
∴∠DOP=∠EOP,
在△DOP和△EOP中
∴△DOP≌△EOP,
∴PD=PE;
(2)解:点P在∠AOB的平分线上,
理由是:
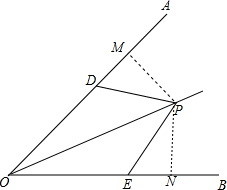
过P作PM⊥OA于M,PN⊥OB于N,
则∠PMD=∠PNE=90°,
∵∠MDP+∠PDO=180°,∠PEN+∠PEO=180°,∠PDO=∠PEO,
∴∠MDP=∠NEP,
在△PMD和△PNE中
∴△PMD≌△PNE(AAS),
∴PM=PN,
∵PM⊥OA,PN⊥OB,
∴点P在∠AOB的平分线上.
理由是:∵P为∠AOB的平分线上一点,
∴∠DOP=∠EOP,
在△DOP和△EOP中
|
∴△DOP≌△EOP,
∴PD=PE;
(2)解:点P在∠AOB的平分线上,
理由是:

过P作PM⊥OA于M,PN⊥OB于N,
则∠PMD=∠PNE=90°,
∵∠MDP+∠PDO=180°,∠PEN+∠PEO=180°,∠PDO=∠PEO,
∴∠MDP=∠NEP,
在△PMD和△PNE中
|
∴△PMD≌△PNE(AAS),
∴PM=PN,
∵PM⊥OA,PN⊥OB,
∴点P在∠AOB的平分线上.
点评:本题考查了全等三角形的性质和判定,角平分线性质的应用,主要考查学生运用性质进行推理的能力.

练习册系列答案
相关题目
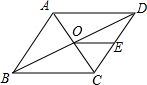 如图,平行四边形ABCD中,对角线AC和BD相交于点O,点E是边CD的中点,连接OE.若AD=5cm,则OE的长度是( )
如图,平行四边形ABCD中,对角线AC和BD相交于点O,点E是边CD的中点,连接OE.若AD=5cm,则OE的长度是( )| A、2cm | B、2.5cm |
| C、3cm | D、3.5cm |