题目内容
已知⊙O的直径为16cm，点E是⊙O内任意一点，
（1）作出过点E的⊙O的最短的弦；
（2）若OE=4cm，则最短弦的长度是多少？
（1）作出过点E的⊙O的最短的弦；
（2）若OE=4cm，则最短弦的长度是多少？
考点：垂径定理,勾股定理
专题：
分析：（1）连接OE，过点E作CD⊥OE分别交⊙O于点C、D，则弦CD即为所求；
（2）连接OC，根据勾股定理求出CE的长，进而可得出CD的长．
（2）连接OC，根据勾股定理求出CE的长，进而可得出CD的长．
解答：
解：（1）如图所示：
（2）连接OC，
∵⊙O的直径为16cm，
∴OC=8cm，
∵OE⊥CD，OE=4cm，
∴CE=
CD，
∴CE=
=
=4
cm，
∴CD=8
cm．
解：（1）如图所示：（2）连接OC，
∵⊙O的直径为16cm，
∴OC=8cm，
∵OE⊥CD，OE=4cm，
∴CE=
| 1 |
| 2 |
∴CE=
| OC2-OE2 |
| 82-42 |
| 3 |
∴CD=8
| 3 |
点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
若y=（m-1）xm2+1+3x+1是二次函数，则m的值是（ ）
| A、1 | B、-1 | C、±1 | D、0 |
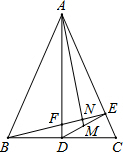如图，在△ABC中，AB=AC，AD⊥BC于点D，DE⊥AC于点E，M为DE中点，AM与BE相交于点N，AD与BE相交于点F．求证：
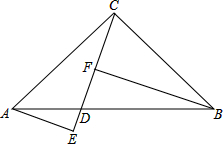已知，在△ABC中，CA=CB，∠C=90°，D为AB上任意一点，AE⊥CD，垂足为E，BF⊥CD，垂足为F，求证：EF=|AE-BF|．
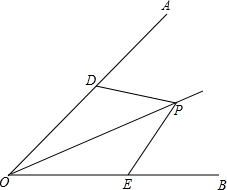（1）如图，P为∠AOB的平分线上一点，点D、E分别在边OA、OB上．若∠PDO=∠PEO，则是否有PD=PE？为什么？