题目内容

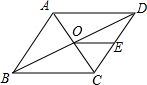如图，平行四边形ABCD中，对角线AC和BD相交于点O，点E是边CD的中点，连接OE．若AD=5cm，则OE的长度是（　　）
A、2cmB、2.5cm
C、3cmD、3.5cm
考点：三角形中位线定理,平行四边形的性质
专题：
分析：首先根据平行四边形的性质可得AO=CO，再根据三角形的中位线定理可得EO=
1
2
AD，进而可得答案．
解答：解：∵四边形ABCD是平行四边形，
∴AO=CO，
∵点E是边CD的中点，
∴EO=
1
2
AD，
∵AD=5cm，
∴EO=2.5cm，
故选：B．
点评：此题主要考查了三角形中位线的性质，关键是掌握三角形的中位线平行于第三边，并且等于第三边的一半．
练习册系列答案
相关题目
把方程2x-y=5变形，用含x的代数式表示y=
 
；用含y的代数式表示x=
 
．
若y=（m-1）xm2+1+3x+1是二次函数，则m的值是（　　）
A、1B、-1C、±1D、0
如图，用尺规作出∠OBF=∠AOB，所画痕迹
MN
是（　　）
A、以点B为圆心，OD为半径的弧
B、以点C为圆心，DC为半径的弧
C、以点E为圆心，OD为半径的弧
D、以点E为圆心，DC为半径的弧
如图，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC=12，BD=5，则该梯形的面积是（　　）
A、30
B、15
C、
15
2
D、60
计算或化简
（1）
9
-（
1
3
）-1-（-1）2013-（-2）0
（2）
2
b
ab3
•（-
3
2
a2b
÷3
b
a
）（a＞0，b＞0）
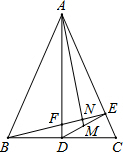如图，在△ABC中，AB=AC，AD⊥BC于点D，DE⊥AC于点E，M为DE中点，AM与BE相交于点N，AD与BE相交于点F．求证：
（1）
DE
CE
=
AD
CD
；
（2）△BCM∽△ADM；
（3）AM⊥BE．
因式分解：
（1）4xy2-4x2y-y3；
（2）2m2nt2-12m2nt+18m2n；
（3）3ax2-15ax+12a．
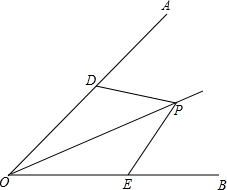（1）如图，P为∠AOB的平分线上一点，点D、E分别在边OA、OB上．若∠PDO=∠PEO，则是否有PD=PE？为什么？
（2）如图，点D、E分别在∠AOB的边OA、OB上，点P在∠AOB内部，∠PDO=∠PEO，且PD=PE，则点P在∠AOB的平分线上吗？为什么？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网