题目内容
长为1、2、3、4、5、6的线段各一条,从6条线段中任选3跳,能构成钝角三角形的概率是多少?
考点:列表法与树状图法
专题:
分析:由从长度分别为1,2,3,4,5,6的六条线段中,任取三条,所有的情况共有20种,满足构成钝角三角形的取法只有:2、3、4;2、4、5;2,5,6;3,4,6;3,5,6共5种,直接利用概率公式求解即可求得答案.
解答:解:从长度分别为1,2,3,4,5,6的六条线段中,任取三条,所有的情况共有20种,
其中,取出的三边能构成钝角三角形时,必须较小的两个边的平方和小于第三边的平方,
故满足构成钝角三角形的取法只有:2、3、4;2、4、5;2,5,6;3,4,6;3,5,6共5种,
故取出的三条线段为边能构成钝角三角形的概率是:
=
,
其中,取出的三边能构成钝角三角形时,必须较小的两个边的平方和小于第三边的平方,
故满足构成钝角三角形的取法只有:2、3、4;2、4、5;2,5,6;3,4,6;3,5,6共5种,
故取出的三条线段为边能构成钝角三角形的概率是:
| 5 |
| 20 |
| 1 |
| 4 |
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
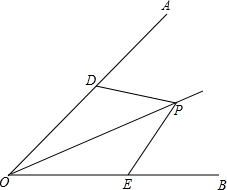 (1)如图,P为∠AOB的平分线上一点,点D、E分别在边OA、OB上.若∠PDO=∠PEO,则是否有PD=PE?为什么?
(1)如图,P为∠AOB的平分线上一点,点D、E分别在边OA、OB上.若∠PDO=∠PEO,则是否有PD=PE?为什么? 如图,已知E、F是线段AB外异侧的两点,EA=EB,FA=FB.求证:EF垂直平分线段AB.
如图,已知E、F是线段AB外异侧的两点,EA=EB,FA=FB.求证:EF垂直平分线段AB. 如图,AD为△ABC边BC上的高,E、F、G分别为AB、BC、AC的中点,求证:FG=DE.
如图,AD为△ABC边BC上的高,E、F、G分别为AB、BC、AC的中点,求证:FG=DE.