题目内容
15.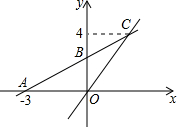 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数y=$\frac{4}{3}x$的图象交于点C(m,4),求m的值及点B的坐标.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数y=$\frac{4}{3}x$的图象交于点C(m,4),求m的值及点B的坐标.
分析 把点C(m,4)代入正比例函数y=$\frac{4}{3}x$的解析式得,m=3,从而求出m的值,然后根据待定系数法求出AC解析式,从而得到B点坐标.
解答 解:把点C(m,4)代入正比例函数y=$\frac{4}{3}x$的解析式得,
m=3,
点C坐标为(3,4),
把A(-3,0),C(3,4)分别代入y=kx+b得,
$\left\{\begin{array}{l}{-3k+b=0}\\{3k+b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=2}\end{array}\right.$,
函数解析式为y=$\frac{2}{3}$x+2.
当x=0时,y=2,则B点坐标为(0,2).
点评 本题考查了两直线相交的问题,熟悉待定系数法是解题的关键.

练习册系列答案
相关题目
6.下列各数是无理数的是( )
| A. | 3.1415926 | B. | $\root{3}{8}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | $\sqrt{\frac{64}{121}}$ |
3.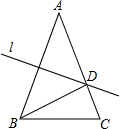 如图,AB=AC=5cm,BC=3cm,直线l是AB的垂直平分线,AC与l相交于点D,则△BDC的周长是( )
如图,AB=AC=5cm,BC=3cm,直线l是AB的垂直平分线,AC与l相交于点D,则△BDC的周长是( )
 如图,AB=AC=5cm,BC=3cm,直线l是AB的垂直平分线,AC与l相交于点D,则△BDC的周长是( )
如图,AB=AC=5cm,BC=3cm,直线l是AB的垂直平分线,AC与l相交于点D,则△BDC的周长是( )| A. | 10 cm | B. | 11 cm | C. | 6 cm | D. | 8 cm |
10.下列运算正确的是( )
| A. | $\sqrt{(-3)^{2}}$=3 | B. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ | D. | $\sqrt{5}$-$\sqrt{2}$=$\sqrt{3}$ |
20.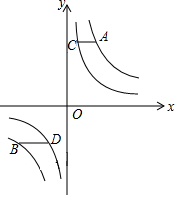 如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )
如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )
 如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )
如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{9}{5}$ | D. | $\frac{12}{5}$ |
4.抛物线y=-3(x+1)2+3的顶点坐标是( )
| A. | (-1,3) | B. | (1,3) | C. | (-1,-3) | D. | (0,3) |
5. 如图所示,△ABC的各个顶点都在正方形的格点上,则sinA的值为( )
如图所示,△ABC的各个顶点都在正方形的格点上,则sinA的值为( )
 如图所示,△ABC的各个顶点都在正方形的格点上,则sinA的值为( )
如图所示,△ABC的各个顶点都在正方形的格点上,则sinA的值为( )| A. | $\frac{\sqrt{10}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{10}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |