题目内容
8.若a≠0,b≠0,则$\frac{|a|}{a}$+$\frac{b}{|b|}$的值为0或±2.分析 要对a,b所有可能出现的不同情况进行分类讨论,找出符合要求的取值,代入求值.
解答 解:对a,b的取值情况分类讨论如下:
①当a,b都是正数时,原式=$\frac{a}{a}+\frac{b}{b}$=1+1=2;
②当a,b都是负数时,原式=$\frac{-a}{a}+\frac{b}{-b}$=-1+(-1)=-2;
③当a,b中有一个正数,一个负数时,$\frac{|a|}{a}$、$\frac{b}{|b|}$中有一个1,一个-1,所以和为0.
故答案为:0或±2.
点评 本题考查了绝对值,解决本题的关键是进行分类讨论,分类讨论时要全面,要做到不重复不遗漏.规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,?ABCD中,AC、BD交于点O1,作?BCD1O1,连结BD1交AC于点O2,作?BCD2O2,连结BD2交AC于点O3,…以此类推,若AC⊥AD,AD=1,∠ADC=60°,则?BCDnOn的面积是$\frac{\sqrt{3}}{{2}^{n}}$.
如图,?ABCD中,AC、BD交于点O1,作?BCD1O1,连结BD1交AC于点O2,作?BCD2O2,连结BD2交AC于点O3,…以此类推,若AC⊥AD,AD=1,∠ADC=60°,则?BCDnOn的面积是$\frac{\sqrt{3}}{{2}^{n}}$. 已知反比例函数y=$\frac{k}{x}$图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,-1),
已知反比例函数y=$\frac{k}{x}$图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,-1), 如图,在△ABC中,∠A=90°,BD是角平分线,若AB=8,BC=10,S△ABD=$\frac{32}{3}$,求△BDC的面积.
如图,在△ABC中,∠A=90°,BD是角平分线,若AB=8,BC=10,S△ABD=$\frac{32}{3}$,求△BDC的面积.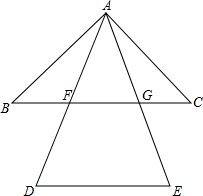 如图,已知△ABC和△ADE都是等腰三角形,AB=AC,AD=AE且∠DAB=∠EAC,则DE∥BC吗?为什么?
如图,已知△ABC和△ADE都是等腰三角形,AB=AC,AD=AE且∠DAB=∠EAC,则DE∥BC吗?为什么?