题目内容
13. 已知反比例函数y=$\frac{k}{x}$图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,-1),
已知反比例函数y=$\frac{k}{x}$图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C(n,-1),(1)求反比例函数的解析式和直线y=ax+b解析式.
(2)求△AOC的面积.
分析 (1)根据Rt△AOB面积为3,A(-2,m)即可求出A点的坐标,把A点坐标代入反比例函数解析式中,求出k的值,又知反比例函数图象过C点(n,-1),代入解析式求出n的值,根据题干条件直线y=ax+b经过点A、C,已知两点坐标,列出二元一次方程组解得a和b的值,即可求出直线y=ax+b的解析式;
(2)根据直线的解析式求出与x轴的交点M的坐标,从而得到OM的长度,再根据S△AOC=S△AOM+S△COM,列式计算即可得解.
解答 解:(1)∵Rt△AOB面积为3,A(-2,m),
∴AB=3,即m=3,
∴A(-2,3),
∵反比例函数为y=$\frac{k}{x}$过点A(-2,3),
∴k=-6,即反比例函数为:y=$\frac{6}{x}$,
∵反比例函数为y=$\frac{6}{x}$过点C(n,-1),
∴n=6,
∴C(6,-1),
∵直线y=ax+b经过点A、C
∴$\left\{\begin{array}{l}{-2a+b=3}\\{6a+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线AC的解析式为:$y=-\frac{1}{2}x+2$;
(2)当y=0时,-$\frac{1}{2}$x+2=0,
解得x=4,
∴点M的坐标为(4,0),
∴OM=4,
S△AOC=S△AOM+S△COM,
=$\frac{1}{2}$×4×3+$\frac{1}{2}$×4×1,
=8.
点评 本题考查了反比例函数与一次函数的交点问题,主要利用了反比例函数解析式系数的几何意义,反比例函数图象的性质,待定系数法求函数解析式,以及三角形的面积的求解,根据系数的几何意义求出k值是解题的关键.

 阅读快车系列答案
阅读快车系列答案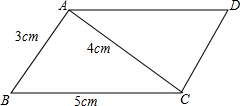 求如图所示的平行四边形ABCD的面积=12cm2.
求如图所示的平行四边形ABCD的面积=12cm2. 如图,已知一次函数y=k1x+b的图象与反比例函数y=$\frac{k_2}{x}$的图象交于A(1,-2),B(2,m)两点,连接OA、OB.
如图,已知一次函数y=k1x+b的图象与反比例函数y=$\frac{k_2}{x}$的图象交于A(1,-2),B(2,m)两点,连接OA、OB.