题目内容
13.△ABC中,AD是BC边上的高,且AB=5,CD=1,sin∠BAD=$\frac{3}{5}$,则BC的边为( )| A. | 4 | B. | 2 | C. | 5 | D. | 2或4 |
分析 分两种情况:①点D在BC边上,如图1,由AD是△ABC边BC上的高,得到∠ADB=90°,根据sin∠BAD=$\frac{BD}{AB}$=$\frac{3}{5}$,求得BD=3,于是得到结论;②点D在直线BC上,如图2,同理得到结论.
解答  解:①点D在BC边上,如图1,∵AD是△ABC边BC上的高,
解:①点D在BC边上,如图1,∵AD是△ABC边BC上的高,
∴∠ADB=90°,
∵sin∠BAD=$\frac{BD}{AB}$=$\frac{3}{5}$,
∵AB=5,
∴BD=3,
∴BC=BD+CD=4,;
②点D在直线BC上,如图2,
∵AD是△ABC边BC上的高,
∴∠ADB=90°,
∵sin∠BAD=$\frac{BD}{AB}$=$\frac{3}{5}$,
∵AB=5,
∴BD=3,
∴BC=BD-CD=2.
故选D.
点评 本题考查了解直角三角形的知识,勾股定理,注意熟练掌握锐角三角函数的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.某养殖户的养殖成本逐年增长,已知第1年的养殖成本为13万元,第3年的养殖成本为20万元.设每年平均增长的百分率为x,则下面所列方程中正确的是( )
| A. | 13(1-x)2=20 | B. | 20(1-x)2=13 | C. | 20(1+x)2=13 | D. | 13(1+x)2=20 |
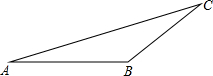 如图,在△ABC中,AB=BC,∠A=15°,求tanA的值.
如图,在△ABC中,AB=BC,∠A=15°,求tanA的值. 用两只完全相同的三角尺在∠AOB的内部如图摆放,两只三角尺较短的直角边必须分别与∠AOB的两边重合,且含30°角的顶点恰好也重合于点C.则射线OC即为∠AOB的角平分线.试利用所学知识说明射线OC平分∠AOB的理由.
用两只完全相同的三角尺在∠AOB的内部如图摆放,两只三角尺较短的直角边必须分别与∠AOB的两边重合,且含30°角的顶点恰好也重合于点C.则射线OC即为∠AOB的角平分线.试利用所学知识说明射线OC平分∠AOB的理由.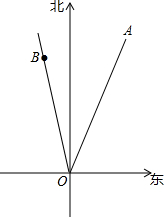 2014年第10号台风“麦德姆”,是2014年度对我国破坏性最大的一次台风,“麦德姆”台风从福建登陆后一路北上,在青岛荣成再次登陆.如图所示,某时,台风“麦德姆”的中心在点O沿北偏东20°的方向以30km/h的速度移动,在点O北偏西10°的方向距离O点360km处有一个小岛B.如果台风中心的最大风力为14级,每远离台风中心20千米风力减弱一级,小岛A的风力达到四级或四级以上,则称其受台风影响.
2014年第10号台风“麦德姆”,是2014年度对我国破坏性最大的一次台风,“麦德姆”台风从福建登陆后一路北上,在青岛荣成再次登陆.如图所示,某时,台风“麦德姆”的中心在点O沿北偏东20°的方向以30km/h的速度移动,在点O北偏西10°的方向距离O点360km处有一个小岛B.如果台风中心的最大风力为14级,每远离台风中心20千米风力减弱一级,小岛A的风力达到四级或四级以上,则称其受台风影响.