题目内容
3.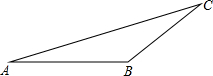 如图,在△ABC中,AB=BC,∠A=15°,求tanA的值.
如图,在△ABC中,AB=BC,∠A=15°,求tanA的值.
分析 过C作CD⊥AB交AB的延长线于D,根据等腰三角形的性质得到∠ACB=∠A=15°,由外角的性质得到∠CBD=∠A+∠ACB=30°,然后根据正切的定义即可得到结论.
解答 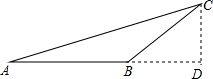 解:过C作CD⊥AB交AB的延长线于D,
解:过C作CD⊥AB交AB的延长线于D,
∵AB=BC,∠A=15°,
∴∠ACB=∠A=15°,
∴∠CBD=∠A+∠ACB=30°,
设CD=a,则BC=AB=2a,BD=$\sqrt{3}$a,
∴AD=(2+$\sqrt{3}$)a,
∴tanA=$\frac{CD}{AD}=\frac{a}{(2+\sqrt{3})a}$=2-$\sqrt{3}$.
点评 本题考查了解直角三角形,等腰三角形的性质,三角形外角的性质,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
12.下列说法正确的是( )
| A. | 4的平方根是±2 | B. | 1的立方根是±1 | ||
| C. | $\sqrt{25}$=±5 | D. | 一个数的算术平方根一定是正数 |
 化简:|a+b|+|b+c|-|a-c|+3|c-b|.
化简:|a+b|+|b+c|-|a-c|+3|c-b|. 如图,已知点D在AC上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,若∠A:∠C=7:4,求∠DBC的度数.
如图,已知点D在AC上,点B在AE上,△ABC≌△DBE,且∠BDA=∠A,若∠A:∠C=7:4,求∠DBC的度数.