题目内容
4.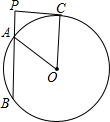 如图,PB是半径为5的圆O的一条割线,PA,PB的长是方程x2-10x+16=0的两个根(PA<PB),PC是圆O的一条切线,C是切点.则四边形PAOC的面积是14.
如图,PB是半径为5的圆O的一条割线,PA,PB的长是方程x2-10x+16=0的两个根(PA<PB),PC是圆O的一条切线,C是切点.则四边形PAOC的面积是14.
分析 连接PO,过点O作OD⊥AB于点D,分别求出△PCO和△AOP的面积,即可得到则四边形PAOC的面积.
解答 解:连接PO,过点O作OD⊥AB于点D,
∵x2-10x+16=(x-2)(x-8)=0,
∴x=2或8,
∵PA,PB的长是方程x2-10x+16=0的两个根(PA<PB),
∴PA=2,PB=8,
∵PB是半径为5的圆O的一条割线,PC是圆O的一条切线,
∴PC2=PA•PB,
∴PC=4,
∴S△PCO=$\frac{1}{2}$PC•OC=10,
∵AB=6,
∴AD=3,
∴OD=4,
∴S△PAO=$\frac{1}{2}$PA•OD=4,
∴四边形PAOC的面积=4+10=14,
故答案为:14.
点评 本题考查了切线的性质、用因式分解法解一元二次方程、切割线定理的运用、勾股定理的运用以及三角形面积公式的运用,正确的添加辅助线把四边形的面积分割为两个三角形的面积是解题关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.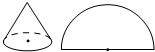 如图,一个圆锥的侧面展开图是半径为10的半圆,则它的底面半径是( )
如图,一个圆锥的侧面展开图是半径为10的半圆,则它的底面半径是( )
 如图,一个圆锥的侧面展开图是半径为10的半圆,则它的底面半径是( )
如图,一个圆锥的侧面展开图是半径为10的半圆,则它的底面半径是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
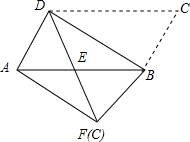 如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E. 如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=6,PB=2,PC=4,求证:∠BPC=135°.
如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=6,PB=2,PC=4,求证:∠BPC=135°.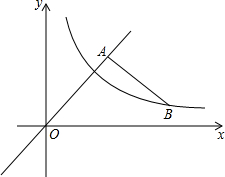 如图,已知A为直线y=x上一点,过A作BA⊥OA交双曲线y=$\frac{k}{x}$于B,若OA2-AB2=8,求k的值.
如图,已知A为直线y=x上一点,过A作BA⊥OA交双曲线y=$\frac{k}{x}$于B,若OA2-AB2=8,求k的值.