题目内容
14.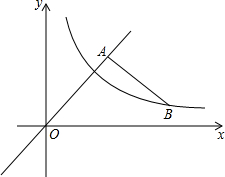 如图,已知A为直线y=x上一点,过A作BA⊥OA交双曲线y=$\frac{k}{x}$于B,若OA2-AB2=8,求k的值.
如图,已知A为直线y=x上一点,过A作BA⊥OA交双曲线y=$\frac{k}{x}$于B,若OA2-AB2=8,求k的值.
分析 延长AB交x轴于C点,作AF⊥x轴于F点,BE⊥x轴于E点,由于直线y=x为第一、三限的角平分线,则△AOB、△BEC为等腰直角三角形,根据等腰直角三角形的性质得AC=AO=$\sqrt{2}$AF,BC=$\sqrt{2}$BE=$\sqrt{2}$CE,AF=$\frac{1}{2}$OC,可得到AB=AC-BC=$\sqrt{2}$(AF-BE),利用OA2-AB2=8变形得2AF•BE-BE2=4,即BE(2AF-BE)=4,由于OC=2AF,BE=EC,所以BE•OE=4,则得到B点的横纵坐标之积为4,从而得到k的值为4.
解答 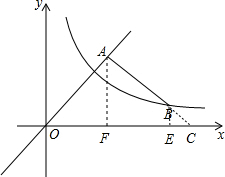 解:延长AB交x轴于C点,作AF⊥x轴于F点,BE⊥x轴于E点,如图,
解:延长AB交x轴于C点,作AF⊥x轴于F点,BE⊥x轴于E点,如图,
∵点A为直线y=x上一点,
∴∠AOC=90°,
∵AB⊥直线y=x,
∴△AOC、△BEC为等腰直角三角形,
∴AC=AO=$\sqrt{2}$AF,BC=$\sqrt{2}$BE=$\sqrt{2}$CE,AF=$\frac{1}{2}$OC,
∴AB=AC-BC=$\sqrt{2}$(AF-BE),
∵OA2-AB2=8,
∴($\sqrt{2}$AF)2-[$\sqrt{2}$(AF-BE)]2=8,
整理得2AF•BE-BE2=4,
∴BE(2AF-BE)=4,
∴BE(OC-CE)=4,即BE•OE=4,
设B点坐标为(x,y),则BE=y,OE=x,
∴BE•OE=xy=4,
∴xy=4,
∴k=4.
点评 本题考查了反比例函数的综合题:反比例函数图象上点的坐标满足其解析式;熟练运用等腰直角三角形的性质解决几何计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.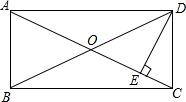 如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且DE=2$\sqrt{2}$,则AC的长是( )
如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且DE=2$\sqrt{2}$,则AC的长是( )
 如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且DE=2$\sqrt{2}$,则AC的长是( )
如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且DE=2$\sqrt{2}$,则AC的长是( )| A. | 4 | B. | 8 | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
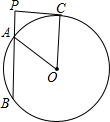 如图,PB是半径为5的圆O的一条割线,PA,PB的长是方程x2-10x+16=0的两个根(PA<PB),PC是圆O的一条切线,C是切点.则四边形PAOC的面积是14.
如图,PB是半径为5的圆O的一条割线,PA,PB的长是方程x2-10x+16=0的两个根(PA<PB),PC是圆O的一条切线,C是切点.则四边形PAOC的面积是14.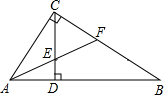 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB,交CD于E,交BC于F,若AF=BF,求证:△CEF是等边三角形.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB,交CD于E,交BC于F,若AF=BF,求证:△CEF是等边三角形.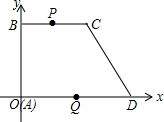 如图,在平面直角坐标系中,梯形ABCD的坐标为A(0,0),B(0,8),C(8,8),D(12,0).点P,Q分别从B,D出发以1个单位/秒和2个单位/秒的速度向C,O运动,设运动时间为t(s)(一点到达,另一点也停止运动).
如图,在平面直角坐标系中,梯形ABCD的坐标为A(0,0),B(0,8),C(8,8),D(12,0).点P,Q分别从B,D出发以1个单位/秒和2个单位/秒的速度向C,O运动,设运动时间为t(s)(一点到达,另一点也停止运动). 如图,AD是△ABC的中线,E、F分别是AB、AC的中点,求证:四边形AEDF是平行四边形.
如图,AD是△ABC的中线,E、F分别是AB、AC的中点,求证:四边形AEDF是平行四边形.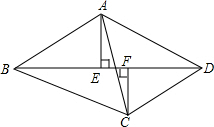 如图,在四边形ABCD中,AE⊥BD,CF⊥BD,且AE=CF,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AE⊥BD,CF⊥BD,且AE=CF,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.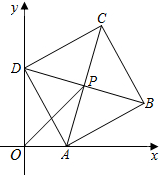 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.设点P到y轴的距离为d,则在点A,D运动的过程中,d的取值范围是2<d≤2$\sqrt{2}$.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.设点P到y轴的距离为d,则在点A,D运动的过程中,d的取值范围是2<d≤2$\sqrt{2}$.