题目内容
9.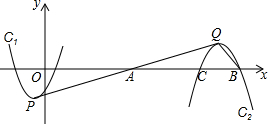 如图,抛物线C1:y=x2+2x-3的顶点为P,将该抛物线绕点A(a,0)(a>0)旋转180°后得到的抛物线C2,抛物线C2的顶点为Q,与x轴的交点是B、C,点B在点C的右侧.若∠PQB=90°,则a=7.
如图,抛物线C1:y=x2+2x-3的顶点为P,将该抛物线绕点A(a,0)(a>0)旋转180°后得到的抛物线C2,抛物线C2的顶点为Q,与x轴的交点是B、C,点B在点C的右侧.若∠PQB=90°,则a=7.
分析 先求出抛物线C1的顶点P的坐标及与x轴的交点坐标,再根据旋转的性质求出抛物线C2的顶点Q的坐标和B点坐标,由于∠PQB=90°,然后根据勾股定理列方程求解.
解答 解:如图所示,
∵y=x2+2x-3=(x+1)2-4,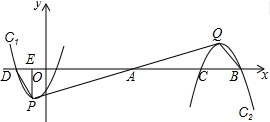
∴P(-1,-4),
∴PD=2$\sqrt{5}$,
令y=0,则x2+2x-3=0,解得:x=-3或x=1,
∴D(-3,0),
∵A(a,0),
∴AD=a+3,AB=a+3,
∵△APD≌△AQB,
∴∠AQB=∠APD=90°,BQ=PD=2$\sqrt{5}$,
∴AP2=AD2-PD2=a2+6a-11=AQ2,
在Rt△ABQ中,AQ2=AB2-BQ2,
∴4+(1+a)2=(a+3)2-(2$\sqrt{5}$)2,
解得:a=7,
故答案为:7.
点评 本题考查了二次函数图象与几何变换,难度较大,求出旋转后的抛物线C2的顶点坐标是解题的关键,也是本题的难点.

练习册系列答案
相关题目
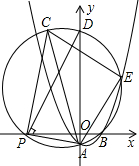 如图,在平面直角坐标系中,抛物线y═$\frac{1}{2}$x2+bx+c经过点A(0,-1),B(2,0)P(t,0)是x轴负半轴上一动点,过点P作PA的垂线交△PAB的外接圆于点C,△PAB的外接圆与y轴交于点D,与抛物线在第一象限限交于点E.
如图,在平面直角坐标系中,抛物线y═$\frac{1}{2}$x2+bx+c经过点A(0,-1),B(2,0)P(t,0)是x轴负半轴上一动点,过点P作PA的垂线交△PAB的外接圆于点C,△PAB的外接圆与y轴交于点D,与抛物线在第一象限限交于点E.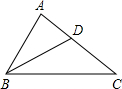 如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
如图,在△ABC中,BD平分∠ABC,∠A=2∠C.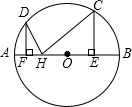 如图,AB是⊙O的直径,C、D是⊙O上的两点,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F、H为EF上的任意一点,若AB=10,CE=4,DF=3,则CH+DH的最小值是7$\sqrt{2}$.
如图,AB是⊙O的直径,C、D是⊙O上的两点,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F、H为EF上的任意一点,若AB=10,CE=4,DF=3,则CH+DH的最小值是7$\sqrt{2}$.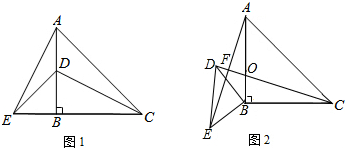
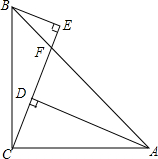 如图,AD=CE=24,BC=25,BE∥AD.BF:AF=7:24,给出下列结论:
如图,AD=CE=24,BC=25,BE∥AD.BF:AF=7:24,给出下列结论: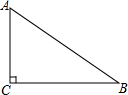 如图,已知△ABC,∠C=Rt∠,AC<BC.D为BC上一点,且到A,B两点的距离相等.
如图,已知△ABC,∠C=Rt∠,AC<BC.D为BC上一点,且到A,B两点的距离相等.