题目内容
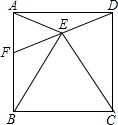 在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.(1)求证:△AEB≌△DEC;
(2)当EB=BC时,求∠AFD的度数.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据正方形的四条边都相等可得AB=CD,每一个角都是直角可得∠BAD=∠ADC=90°,再根据直角三角形斜边上的中线等于斜边的一半可得AE=EF=DE=
DF,根据等边对等角可得∠EAD=∠EDA,再求出∠BAE=∠CDE,然后利用“边角边”证明即可;
(2)根据全等三角形对应边相等可得EB=EC,再求出△BCE是等边三角形,根据等边三角形的性质可得∠EBC=60°,然后求出∠ABE=30°,再根据等腰三角形两底角相等求出∠BAE,然后根据等边对等角可得∠AFD=∠BAE.
| 1 |
| 2 |
(2)根据全等三角形对应边相等可得EB=EC,再求出△BCE是等边三角形,根据等边三角形的性质可得∠EBC=60°,然后求出∠ABE=30°,再根据等腰三角形两底角相等求出∠BAE,然后根据等边对等角可得∠AFD=∠BAE.
解答:(1)证明:在正方形ABCD中,AB=CD,∠BAD=∠ADC=90°,
∵点E为DF中点,
∴AE=EF=DE=
DF,
∴∠EAD=∠EDA,
∵∠BAE=∠BAD-∠EAD,∠CDE=∠ADC-∠EDA,
∴∠BAE=∠CDE,
在△AEB和△DEC中,
,
∴△AEB≌△DEC(SAS);
(2)解:∵△AEB≌△DEC,
∴EB=EC,
∵EB=BC,
∴EB=BC=EC,
∴△BCE是等边三角形,
∴∠EBC=60°,
∴∠ABE=90°-60°=30°,
∵EB=BC=AB,
∴∠BAE=
(180°-30°)=75°,
又∵AE=EF,
∴∠AFD=∠BAE=75°.
∵点E为DF中点,
∴AE=EF=DE=
| 1 |
| 2 |
∴∠EAD=∠EDA,
∵∠BAE=∠BAD-∠EAD,∠CDE=∠ADC-∠EDA,
∴∠BAE=∠CDE,
在△AEB和△DEC中,
|
∴△AEB≌△DEC(SAS);
(2)解:∵△AEB≌△DEC,
∴EB=EC,
∵EB=BC,
∴EB=BC=EC,
∴△BCE是等边三角形,
∴∠EBC=60°,
∴∠ABE=90°-60°=30°,
∵EB=BC=AB,
∴∠BAE=
| 1 |
| 2 |
又∵AE=EF,
∴∠AFD=∠BAE=75°.
点评:本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,等角的余角相等的性质,等边三角形的判定与性质,难点在于(2)求出等边三角形.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知x=1是方程x2=ax+2的一个根,则此方程的另一个根为( )
| A、-2 | B、-1 | C、0 | D、1 |
如图,第①个图有2个相同的小正方形,第②个图有6个相同的小正方形,第③个图有12个相同的小正方形,…,按此规律,那么第15个图中小正方形的个数是( )
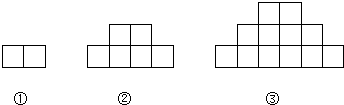

| A、225 | B、240 |
| C、30 | D、255 |
 如图,在Rt△ABC中,AC⊥BC,D为AB上任意一点,过A、C分别作AB、CD的垂线相交于点E,tanB=
如图,在Rt△ABC中,AC⊥BC,D为AB上任意一点,过A、C分别作AB、CD的垂线相交于点E,tanB=
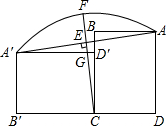 如图,将矩形ABCD向左绕点C推倒,恰好D落在BC上D′处,得到矩形A′B′C′D′,作CE⊥AA′交
如图,将矩形ABCD向左绕点C推倒,恰好D落在BC上D′处,得到矩形A′B′C′D′,作CE⊥AA′交

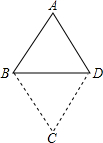 如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:
如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题: 如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.求点P到海岸线l的距离;(结果保留根号)
如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.求点P到海岸线l的距离;(结果保留根号)