题目内容
 如图,在Rt△ABC中,AC⊥BC,D为AB上任意一点,过A、C分别作AB、CD的垂线相交于点E,tanB=
如图,在Rt△ABC中,AC⊥BC,D为AB上任意一点,过A、C分别作AB、CD的垂线相交于点E,tanB=| 5 |
| 2 |
(1)求证:△AEC∽△BDC;
(2)求S△AEC:S△BDC.
考点:相似三角形的判定与性质
专题:
分析:(1)欲证明△AEC∽△BDC,只需证明∠EAC=∠B,∠ECA=∠BCD.
(2)利用相似三角形面积的比等于其相似比的平方,结合直角三角形的边角关系即可解决问题.
(2)利用相似三角形面积的比等于其相似比的平方,结合直角三角形的边角关系即可解决问题.
解答:解(1)∵AE⊥AB,AC⊥BC,
∴∠EAC+∠CAB=∠B+∠CAB=90°,
故∠EAC=∠B;
又∵CE⊥CD,AC⊥BC,
∴∠ECA+∠ACD=∠BCD+∠ACD,故∠ECA=∠BCD;
而∠EAC=∠B,
∴△AEC∽△BDC.
(2)∵△AEC∽△BDC,
∴S
=(
)2;
而tanB=
=
,
∴
=
,
即S△AEC:S△BDC=
.
∴∠EAC+∠CAB=∠B+∠CAB=90°,
故∠EAC=∠B;
又∵CE⊥CD,AC⊥BC,
∴∠ECA+∠ACD=∠BCD+∠ACD,故∠ECA=∠BCD;
而∠EAC=∠B,
∴△AEC∽△BDC.
(2)∵△AEC∽△BDC,
∴S
| S△AEC |
| S△BDC |
| AC |
| BC |
而tanB=
| AC |
| BC |
| 5 |
| 2 |
∴
| S△AEC |
| S△BDC |
| 25 |
| 4 |
即S△AEC:S△BDC=
| 25 |
| 4 |
点评:考查了相似三角形的判定及其性质的应用问题;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,已知直线a,b被直线c所截,a∥b,∠2=50°,则∠1=( )
如图,已知直线a,b被直线c所截,a∥b,∠2=50°,则∠1=( )| A、50° | B、130° |
| C、40° | D、60° |
把数12.348精确到十分位为( )
| A、12.4 | B、12.3 |
| C、12.35 | D、12.34 |

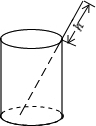 如图,将一根长12厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为
如图,将一根长12厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为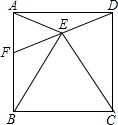 在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.