题目内容
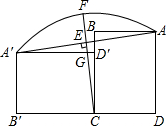 如图,将矩形ABCD向左绕点C推倒,恰好D落在BC上D′处,得到矩形A′B′C′D′,作CE⊥AA′交
如图,将矩形ABCD向左绕点C推倒,恰好D落在BC上D′处,得到矩形A′B′C′D′,作CE⊥AA′交 |
| AA′ |
(1)求EF的长;
(2)求GD′的长.
考点:旋转的性质,矩形的性质
专题:
分析:(1)连接AC、A′C,利用勾股定理列式求出AC,根据旋转的性质可得AC=A′C,∠ACA′=90°,判断出△ACA′是等腰直角三角形,再根据等腰直角三角形的性质求出CE,然后根据EF=CF-CE计算即可得解;
(2)求出△A′EG和△CD′G相似,根据相似三角形对应边成比例可得
=
=
=
,设EG=5
k,GD′=6k,表示出A′G、CG,再根据相似比列式求出k,然后求解即可.
(2)求出△A′EG和△CD′G相似,根据相似三角形对应边成比例可得
| EG |
| D′G |
| A′G |
| CG |
| A′E |
| CD′ |
5
| ||
| 6 |
| 2 |
解答: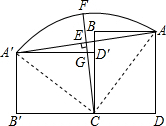 解:(1)如图,连接AC、A′C,
解:(1)如图,连接AC、A′C,
由勾股定理得,AC=
=
=5,
由旋转的性质得,AC=CF=A′C=5,∠ACA′=90°,
∴△ACA′是等腰直角三角形,
∴CE=A′E=
A′C=5×
=
,
∴EF=CF-CE=5-
;
(2)∵∠A′G=∠CD′G=90°,∠A′GE=∠CGD′,
∴△A′EG∽△CD′G,
∴
=
=
=
=
,
设EG=5
k,GD′=6k,
则A′G=4-6k,CG=
-5
k,
∴
=
,
解得k=
,
所以,GD′=6×
=
.
 解:(1)如图,连接AC、A′C,
解:(1)如图,连接AC、A′C,由勾股定理得,AC=
| AB2+BC2 |
| 32+42 |
由旋转的性质得,AC=CF=A′C=5,∠ACA′=90°,
∴△ACA′是等腰直角三角形,
∴CE=A′E=
| ||
| 2 |
| ||
| 2 |
5
| ||
| 2 |
∴EF=CF-CE=5-
5
| ||
| 2 |
(2)∵∠A′G=∠CD′G=90°,∠A′GE=∠CGD′,
∴△A′EG∽△CD′G,
∴
| EG |
| D′G |
| A′G |
| CG |
| A′E |
| CD′ |
| ||||
| 3 |
5
| ||
| 6 |
设EG=5
| 2 |
则A′G=4-6k,CG=
5
| ||
| 2 |
| 2 |
∴
| 4-6k | ||||||
|
5
| ||
| 6 |
解得k=
| 1 |
| 14 |
所以,GD′=6×
| 1 |
| 14 |
| 3 |
| 7 |
点评:本题考查了旋转的性质,矩形的性质,等腰直角三角形的判定与性质,相似三角形的判定与性质,难点在于(2)利用相似比列出比例式.

练习册系列答案
相关题目
把数12.348精确到十分位为( )
| A、12.4 | B、12.3 |
| C、12.35 | D、12.34 |
 如图,A、B、C是⊙O上的三点,且∠ABD=70°,AB=BD,则∠O的度数是( )
如图,A、B、C是⊙O上的三点,且∠ABD=70°,AB=BD,则∠O的度数是( )| A、70° | B、110° |
| C、130° | D、140° |
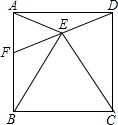 在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE. 如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是
如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是