题目内容
如图,以Rt△ABO的直角顶点O为原点,OA所在的直线为x轴,OB所在直线为y轴,建立平面直角坐标系.已知OA=8,OB=6,一动点P从O出发沿OA方向,以每秒1个单位长度的速度向A点匀速运动,到达A点后立即以原速沿AO返回;点Q从点A出发沿AB以每秒1个单位长度向点B匀速运动,当Q到达B时,P、Q两点同时停止运动.设P、Q运动的时间为t秒(t>0).
(1)当t为何值时,△APQ的面积为
?
(2)在点P从O向A运动的过程中,在y轴上是否存在点E使得四边形PQBE为直角梯形?若存在,求出点E的坐标;若不存在,请说明理由;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB-BO-OP于点F.当DF经过原点O时,写出t的值.

(1)当t为何值时,△APQ的面积为
| 9 |
| 2 |
(2)在点P从O向A运动的过程中,在y轴上是否存在点E使得四边形PQBE为直角梯形?若存在,求出点E的坐标;若不存在,请说明理由;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB-BO-OP于点F.当DF经过原点O时,写出t的值.

考点:一次函数综合题
专题:
分析:(1)过Q作QR⊥x轴交x轴于点R,可用t表示出QR,进一步表示△APQ的面积,令其等于
可求出t,注意分点P由O向A运动和由A向O运动两种情况;
(2)分PE∥BQ和PQ∥PE两种情况,利用条件可以用t表示出相应线段的长度,再利用平行线分线段成比例的性质得到线段之间的比例关系求出t的值,进一步可求出E点的坐标;
(3)由条件可知DF为PQ的垂直平分线,由此可得到线段相等,用t表示出相应线段,求出t即可,注意也需要分点P由O向A运动和由A向O运动两种情况.
| 9 |
| 2 |
(2)分PE∥BQ和PQ∥PE两种情况,利用条件可以用t表示出相应线段的长度,再利用平行线分线段成比例的性质得到线段之间的比例关系求出t的值,进一步可求出E点的坐标;
(3)由条件可知DF为PQ的垂直平分线,由此可得到线段相等,用t表示出相应线段,求出t即可,注意也需要分点P由O向A运动和由A向O运动两种情况.
解答:解:(1)如图1,过Q作QR⊥x轴,交x轴于点R,则QR∥OB,由勾股定理可求得AB=10,

由平行线分线段成比例可得
=
,即
=
,解得QR=
t,
当0<t<8时,OP=AQ=t,则AP=8-t,此时S△APQ=
AP•QR=
(8-t)×
t,
令
(8-t)×
t=
,解得t=3或t=5,
当8≤t<10时,AP=t-8,AQ=t,同理可求得QR=
t,此时S△APQ=
AP•QR=
(t-8)×
t,
令
(t-8)×
t=
,整理得:t2-8t-15=0解得t=4+
或t=4-
(小于0舍去),
综上可知当t的值为3或5或4+
时,△APQ的面积为
;
(2)存在,
由题意可知OP=AQ=t,AP=8-t.
当PE∥BQ,PQ⊥PE时,如图2,

在△EOP和△PQA中
,
所以△EOP≌△PQA,
所以PE=AP=8-t,
又PE∥AB,
由平行线分线段成比例可得:
=
,
即
=
,解得t=
,则PE=8-t=
,
在Rt△POE中,由勾股定理可求得OE=
,即E点坐标为(0,
),
当PQ∥BE,PE⊥BE时,即E为原点,
PE=AQ=t,AP=8-t,则有
=
,即
=
,解得t=
,符合题意,
此时点E的坐标为(0,0),
综上可知存在满足条件的E点,E点的坐标为(0,
)或(0,0);
(3)①当P由O向A运动时,OQ=OP=AQ=t,
可得∠QOA=∠QAO,
所以∠QOB=∠QBO,
所以OQ=BQ=t,
所以BQ=AQ=
AB,
即AB=2t,解得t=5,
②如图3,
当P由A向O运动时,过Q作QG⊥y轴交y轴于点G,

OQ=OP=16-t,BQ=10-t,
则
=
,即
=
,所以GQ=
(10-t),
同理可求得BG=
(10-t),所以GO=6-
(10-t),
在Rt△OGQ中,由勾股定理可得:OG2+GQ2=OQ2,
即[6-
(10-t)]2+[
(10-t)]2=(16-t)2,
解得t=10,
综上可知满足条件的t的值为5和10.

由平行线分线段成比例可得
| QR |
| OB |
| AQ |
| AB |
| QR |
| 6 |
| t |
| 10 |
| 3 |
| 5 |
当0<t<8时,OP=AQ=t,则AP=8-t,此时S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
令
| 1 |
| 2 |
| 3 |
| 5 |
| 9 |
| 2 |
当8≤t<10时,AP=t-8,AQ=t,同理可求得QR=
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
令
| 1 |
| 2 |
| 3 |
| 5 |
| 9 |
| 2 |
| 31 |
| 31 |
综上可知当t的值为3或5或4+
| 31 |
| 9 |
| 2 |
(2)存在,
由题意可知OP=AQ=t,AP=8-t.
当PE∥BQ,PQ⊥PE时,如图2,

在△EOP和△PQA中
|
所以△EOP≌△PQA,
所以PE=AP=8-t,
又PE∥AB,
由平行线分线段成比例可得:
| PE |
| AB |
| OP |
| OA |
即
| 8-t |
| 10 |
| t |
| 8 |
| 32 |
| 9 |
| 40 |
| 9 |
在Rt△POE中,由勾股定理可求得OE=
| 24 |
| 9 |
| 24 |
| 9 |
当PQ∥BE,PE⊥BE时,即E为原点,
PE=AQ=t,AP=8-t,则有
| AP |
| OA |
| AQ |
| AB |
| 8-t |
| 8 |
| t |
| 10 |
| 40 |
| 9 |
此时点E的坐标为(0,0),
综上可知存在满足条件的E点,E点的坐标为(0,
| 24 |
| 9 |
(3)①当P由O向A运动时,OQ=OP=AQ=t,
可得∠QOA=∠QAO,
所以∠QOB=∠QBO,
所以OQ=BQ=t,
所以BQ=AQ=
| 1 |
| 2 |
即AB=2t,解得t=5,
②如图3,
当P由A向O运动时,过Q作QG⊥y轴交y轴于点G,

OQ=OP=16-t,BQ=10-t,
则
| BQ |
| BA |
| GQ |
| OA |
| 10-t |
| 10 |
| GQ |
| 8 |
| 4 |
| 5 |
同理可求得BG=
| 3 |
| 5 |
| 3 |
| 5 |
在Rt△OGQ中,由勾股定理可得:OG2+GQ2=OQ2,
即[6-
| 3 |
| 5 |
| 4 |
| 5 |
解得t=10,
综上可知满足条件的t的值为5和10.
点评:本题主要考查一次函数及平行线分线段成比例的性质,把相应的线段用t表示出来利用平行或垂直或直角三角形中的勾股定理得到关于t的方程是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
把数12.348精确到十分位为( )
| A、12.4 | B、12.3 |
| C、12.35 | D、12.34 |
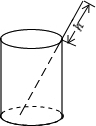 如图,将一根长12厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为
如图,将一根长12厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为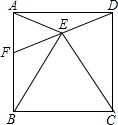 在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.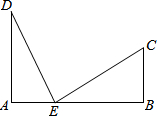 某镇为响应中央关于建设社会主义新农村的号召,决定公路相距25km的A,B两站之间E点修建一个土特产加工基地,如图,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要使C、D两村到E点的距离相等,那么基地E应建在离A站多少km的地方?
某镇为响应中央关于建设社会主义新农村的号召,决定公路相距25km的A,B两站之间E点修建一个土特产加工基地,如图,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要使C、D两村到E点的距离相等,那么基地E应建在离A站多少km的地方?