题目内容
在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.

(1)填写下列各点的坐标:
A1 ,A3 ,A12 ;
(2)设n是4的倍数,写出连续四点An-1,An,An+1,An+2的坐标(n是正整数);
(3)指出蚂蚁从点A100到A101的移动方向.

(1)填写下列各点的坐标:
A1
(2)设n是4的倍数,写出连续四点An-1,An,An+1,An+2的坐标(n是正整数);
(3)指出蚂蚁从点A100到A101的移动方向.
考点:规律型:点的坐标
专题:
分析:(1)观察图形可知,A3,A12都在x轴上,求出OA1、OA3、OA12的长度,然后写出坐标即可;
(2)根据(1)中规律写出点An的坐标即可写出其他各点的坐标;
(3)根据100是4的倍数,可知从点A100到点A101的移动方向与从点O到A1的方向一致.
(2)根据(1)中规律写出点An的坐标即可写出其他各点的坐标;
(3)根据100是4的倍数,可知从点A100到点A101的移动方向与从点O到A1的方向一致.
解答:解:(1)∵蚂蚁每次移动1个单位,
∴OA1=1,OA3=4,OA12=6,
∴A4(0,1),A3(1,0),A12(6,0);
(2)∵n是4的倍数,
∴根据(1)OAn=n÷2=
,
∴点An的坐标(
,0),
∴An-1(
-1),An+1(
,0),An+2(
+1,1);
(3)∵100÷4=25,
∴100是4的倍数,
∴A100 (50,0),
∵101÷4=25…1,
∴A101与A100横坐标相同,
∴A101 (50,1),
∴从点A100到点A101的移动方向与从点O到A1的方向一致,为从下向上.
∴OA1=1,OA3=4,OA12=6,
∴A4(0,1),A3(1,0),A12(6,0);
(2)∵n是4的倍数,
∴根据(1)OAn=n÷2=
| n |
| 2 |
∴点An的坐标(
| n |
| 2 |
∴An-1(
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
(3)∵100÷4=25,
∴100是4的倍数,
∴A100 (50,0),
∵101÷4=25…1,
∴A101与A100横坐标相同,
∴A101 (50,1),
∴从点A100到点A101的移动方向与从点O到A1的方向一致,为从下向上.
点评:此题主要考查了点的变化规律,比较简单,仔细观察图形,确定出A4n都在x轴上是解题的关键.

练习册系列答案
相关题目
如图,下列是由边长为2的等边三角形按照一定规律排列而成,第一个图形的周长为6,第二个所组成图形的周长为8,将若干的等边三角形按照这样的规律来摆放,则第8个图形的周长( )


| A、18 | B、19 | C、20 | D、21 |
 用块完全相同的长方体搭成如图几何体,这个几何体从正面看到的形状是( )
用块完全相同的长方体搭成如图几何体,这个几何体从正面看到的形状是( )A、 |
B、 |
C、 |
D、 |
 如图,作字母N(折线ABCD)关于y轴的轴对称图形,并写出所得图形相对应的坐标.
如图,作字母N(折线ABCD)关于y轴的轴对称图形,并写出所得图形相对应的坐标.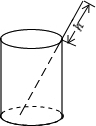 如图,将一根长12厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为
如图,将一根长12厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为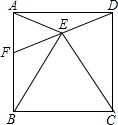 在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.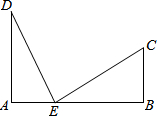 某镇为响应中央关于建设社会主义新农村的号召,决定公路相距25km的A,B两站之间E点修建一个土特产加工基地,如图,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要使C、D两村到E点的距离相等,那么基地E应建在离A站多少km的地方?
某镇为响应中央关于建设社会主义新农村的号召,决定公路相距25km的A,B两站之间E点修建一个土特产加工基地,如图,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要使C、D两村到E点的距离相等,那么基地E应建在离A站多少km的地方?