题目内容
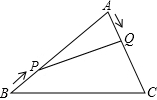 如图,在△ABC中,∠A=60°,AB=18,AC=12,点P从点B出发,以3cm/s的速度向点A运动,点Q从点A同时出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.
如图,在△ABC中,∠A=60°,AB=18,AC=12,点P从点B出发,以3cm/s的速度向点A运动,点Q从点A同时出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.(1)求S△ABC;
(2)在点P与点Q的运动过程中,△APQ是否能成为等边三角形?若能,请求出时间t,若不能,请说明理由;
(3)当t为何值时,△APQ是直角三角形?
考点:勾股定理,等边三角形的判定与性质
专题:动点型
分析:(1)过点C作CD⊥AB于D,根据直角三角形两锐角互余求出∠ACD=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出AD,利用勾股定理列式求出CD,然后利用三角形的面积公式列式计算即可得解;
(2)表示出AP、AQ,然后根据等边三角形的三条边都相等列出方程求解即可;
(3)分PQ⊥AC和PQ⊥AB两种情况,列出方程求解即可.
(2)表示出AP、AQ,然后根据等边三角形的三条边都相等列出方程求解即可;
(3)分PQ⊥AC和PQ⊥AB两种情况,列出方程求解即可.
解答: 解:(1)如图,过点C作CD⊥AB于D,
解:(1)如图,过点C作CD⊥AB于D,
∵∠A=60°,
∴∠ACD=30°,
∴AD=
AC=
×12=6,
由勾股定理得,CD=
=6
,
所以,△ABC的面积=
×18×6
=54
;
(2)能.
∵∠A=60°,AP=AQ,
∴18-3t=2t,
解得t=3.6s;
(3)当PQ⊥AC时,有AQ=
AP,
所以,2t=
(18-3t),
解得t
s;
当PQ⊥AB,有AP=
AQ,
所以,18-3t=
×2t,
解得t=4.5s.
 解:(1)如图,过点C作CD⊥AB于D,
解:(1)如图,过点C作CD⊥AB于D,∵∠A=60°,
∴∠ACD=30°,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理得,CD=
| 122-62 |
| 3 |
所以,△ABC的面积=
| 1 |
| 2 |
| 3 |
| 3 |
(2)能.
∵∠A=60°,AP=AQ,
∴18-3t=2t,
解得t=3.6s;
(3)当PQ⊥AC时,有AQ=
| 1 |
| 2 |
所以,2t=
| 1 |
| 2 |
解得t
| 18 |
| 7 |
当PQ⊥AB,有AP=
| 1 |
| 2 |
所以,18-3t=
| 1 |
| 2 |
解得t=4.5s.
点评:本题考查了勾股定理,直角三角形两锐角互余的性质,直角三角形30°角所对的直角边等于斜边的一半,(3)要分情况讨论.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
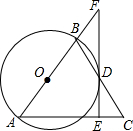 如图在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F,
如图在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F,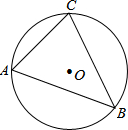 如图,圆O是△ABC的外接圆,圆O的半径为6,∠ABC=45°,求AC的长.
如图,圆O是△ABC的外接圆,圆O的半径为6,∠ABC=45°,求AC的长.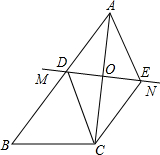 如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD.
如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD.