题目内容
5. 如图,在△ABC中,∠ABC=45°,高AD,BE交于H点,若CD=5,则DH=5.
如图,在△ABC中,∠ABC=45°,高AD,BE交于H点,若CD=5,则DH=5.
分析 先由已知得到BD=AD,即可证明△BDH≌△ADC,即可求得DH=CD.
解答 解:∵∠ABC=45°,AD⊥BC,
∴BD=AD,
∵∠CAD+∠AHE=90°,∠CAD+∠C=90°,∠AHE=∠BHD,
∴∠AHE=∠C,
在△BDH和△ADC中,
$\left\{\begin{array}{l}{∠CAD=∠HBD}\\{AD=BD}\\{∠BDH=∠ADC}\end{array}\right.$,
∴△BDH≌△ADC(ASA),
∴DH=CD=5.
故答案为:5.
点评 本题考查了全等三角形的判定、全等三角形对应边相等的性质.解决本题的根据是证明△BDF≌△ADC.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
10. 如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )
如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )
 如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )
如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
 在△ABC中,DG∥EC,EG∥BC.求证:AE2=AB•AD.
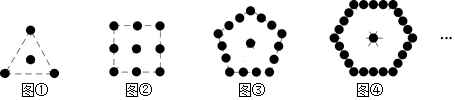
在△ABC中,DG∥EC,EG∥BC.求证:AE2=AB•AD. ”组成,其中第①个图案中有4个,第②个图案中有9个,第③个图案中有16个,第④个图案有25个,…,则第⑨个图案中的个数为( )
”组成,其中第①个图案中有4个,第②个图案中有9个,第③个图案中有16个,第④个图案有25个,…,则第⑨个图案中的个数为( )