题目内容
17.已知实数a、b,满足ab=1,求$\frac{1}{{a}^{2}+1}$+$\frac{1}{{b}^{2}+1}$的值.分析 先根据异分母的分式相加减的法则把原式化简,再把ab=1代入进行计算即可.
解答 解:原式=$\frac{{b}^{2}+1+{a}^{2}+1}{{(a}^{2}+1){(b}^{2}+1)}$
=$\frac{{b}^{2}+{a}^{2}+2}{{(a}^{2}+1){(b}^{2}+1)}$
=$\frac{{a}^{2}+{b}^{2}+2}{{a}^{2}{b}^{2}+{a}^{2}+{b}^{2}+1}$,
∵ab=1,
∴原式=$\frac{{a}^{2}+{b}^{2}+2}{{a}^{2}+{b}^{2}+2}$=1.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.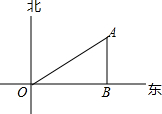 如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
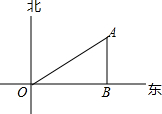 如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )| A. | 250米 | B. | 250$\sqrt{3}$米 | C. | $\frac{500}{3}$$\sqrt{3}$米 | D. | 500$\sqrt{2}$米 |
5.以下是龙湾风景区旅游信息:
根据以上信息,某公司组织一批员工到该风景区旅游,支付给旅行社2800元.从中可以推算出该公司参加旅游的人数为40.
| 旅游人数 | 收费标准 |
| 不超过30人 | 人均收费80元 |
| 超过30人 | 每增加1人,人均收费降低1元,但人均收费不低于50元 |
9.课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果制成了如下的统计表.
(1)a的值为5%;
(2)请你从表格中任意选取一列数据,绘制合理的统计图来表示.(绘制一种即可)
(3)说一说你选择此统计图的理由.

| 等级 | 人数/名 | 百分比 |
| 优秀 | 200 | 20% |
| 良好 | 600 | 60% |
| 及格 | 150 | 15% |
| 不及格 | 50 | a |
(2)请你从表格中任意选取一列数据,绘制合理的统计图来表示.(绘制一种即可)
(3)说一说你选择此统计图的理由.
