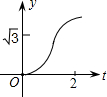题目内容
7.某商场购进甲、乙两种商品,若购买2件甲商品和3件乙商品共需340元,购买4件甲商品和5件乙商品共需600元.(1)求购买一件甲商品和一件乙商品分别需要多少元?
(2)若根据实际情况,商场需一次性购买两种商品共100件,且购买两种商品的总费用不超过7000元,求该商场最多可以购买多少件乙商品.
分析 (1)首先设购买一件甲商品需x元,购买一件乙商品需要y元,由题意得等量关系:①2件甲商品的费用+3件乙商品的费用=340;②4件甲商品的费用+5件乙商品的费用=600,根据等量关系列出方程组,再解即可;
(2)首先设该商场可以购买a件乙商品,则可以购买甲种商品(100-a)件,由题意得不等关系:甲商品的总费用+乙商品的总费用≤7000,再列出不等式,求解即可.
解答 解:(1)设购买一件甲商品需x元,购买一件乙商品需要y元,
根据题意,得:$\left\{\begin{array}{l}{2x+3y=340}\\{4x+5y=600}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=50}\\{y=80}\end{array}\right.$,
答:购买一件甲商品需50元,购买一件乙商品需要80元.
(2)设该商场可以购买a件乙商品,则可以购买甲种商品(100-a)件,
根据题意,得:50(100-a)+80a≤7000
解得:a≤66$\frac{2}{3}$,
答:该商场最多可以购买66件乙商品.
点评 此题主要考查了二元一次方程组和一元一次不等式的应用,关键是正确理解题意,找出题目中的等量关系和不等关系,列出方程组和不等式.

练习册系列答案
相关题目
18.Rt△ABC中,∠C=90°,∠B=44°,则∠A=( )
| A. | 66° | B. | 36° | C. | 56° | D. | 46° |
15.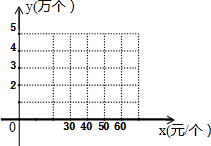 某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:
某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:
同时,销售过程中的其他开支费用总计40万元.
(1)以x作为点的横坐标,y作为点的纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察顺次连结各点所得的图形,判断y与x的函数关系,并求出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净利润w(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元/个时净利润最大,最大值是多少?
(净利润=销售收入-买入支出-其它开支)
(3)该公司要求净利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元/个?
 某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:
某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(1)以x作为点的横坐标,y作为点的纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察顺次连结各点所得的图形,判断y与x的函数关系,并求出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净利润w(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元/个时净利润最大,最大值是多少?
(净利润=销售收入-买入支出-其它开支)
(3)该公司要求净利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元/个?
2.下列命题中正确的是( )
| A. | 有两条边分别相等的两个等腰三角形全等 | |
| B. | 两腰对应相等的两个等腰三角形全等 | |
| C. | 有两条边分别相等的两个直角三角形全等 | |
| D. | 斜边和一条直角边对应相等的两个直角三角形全等 |
12.下列交通标志中,轴对称图形的个数是( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
17. 如图,添加条件不能判断△ACD≌△ABE的是( )
如图,添加条件不能判断△ACD≌△ABE的是( )
 如图,添加条件不能判断△ACD≌△ABE的是( )
如图,添加条件不能判断△ACD≌△ABE的是( )| A. | ∠AEB=∠ADC,CD=BE | B. | AC=AB,AD=AE | C. | AC=AB,∠C=∠B | D. | ∠AEB=∠ADC,∠C=∠B |
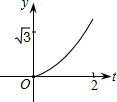
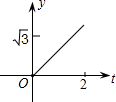
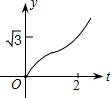
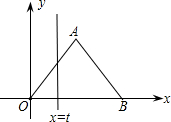 如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )
如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )