题目内容
12.在?ABCD中,BC边上的高为4,AB=5,AC=2$\sqrt{5}$,则?ABCD的周长为20或12.分析 根据题意分两种情况画出图形,BC边上的高在平行四边形的内部和外部,进而利用勾股定理求出即可.
解答 解: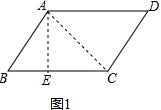 分两种情况:
分两种情况:
①如图1所示:
∵在?ABCD中,BC边上的高AE为4,AB=5,AC=2$\sqrt{5}$,
∴CD=AB=5,AD=BC,EC=$\sqrt{A{C}^{2}-A{E}^{2}}$=2,BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=3,
∴AD=BC=2+3=5,
∴?ABCD的周长=2(AB+BC)=20,
②如图2所示: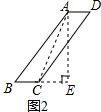
同①得:EC═$\sqrt{A{C}^{2}-A{E}^{2}}$=2,BE═$\sqrt{A{B}^{2}-A{E}^{2}}$=3,
∴AD=BC=3-2=1,
∴?ABCD的周长=2(AB+BC)=12,
综上所述:?ABCD的周长为20或12.
故答案为:20或12.
点评 此题主要考查了平行四边形的性质以及勾股定理等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
4.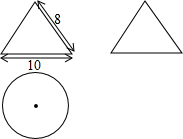 如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )
 如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )| A. | 40πcm2 | B. | 65πcm2 | C. | 80πcm2 | D. | 105πcm2 |
5.下列实数中小于0的数是( )
| A. | 2016 | B. | -2016 | C. | $\sqrt{2016}$ | D. | $\frac{1}{2016}$ |
2.下列命题中正确的是( )
| A. | 有两条边分别相等的两个等腰三角形全等 | |
| B. | 两腰对应相等的两个等腰三角形全等 | |
| C. | 有两条边分别相等的两个直角三角形全等 | |
| D. | 斜边和一条直角边对应相等的两个直角三角形全等 |