题目内容
14.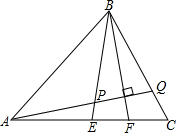 如图,△ABC中,BE为AC边的中线,BF平分∠EBC,AQ⊥BF交BE于P,交BC于Q,求$\frac{EP}{CQ}$.
如图,△ABC中,BE为AC边的中线,BF平分∠EBC,AQ⊥BF交BE于P,交BC于Q,求$\frac{EP}{CQ}$.
分析 作EM∥QC交AQ于M,由三角形的中位线的性质得到EM=$\frac{1}{2}$CQ,且∠EMH=∠BQH,由BF平分∠EBC,BF⊥PQ,得到△BPQ是等腰三角形,根据等腰三角形的性质得到∠BPQ=∠BQP,由对顶角的性质得到∠MPE=∠BPQ,等量代换得到∠EMH=∠MPE,根据等腰三角形的判定得到EP=EM=$\frac{1}{2}$CQ,于是得到结论.
解答 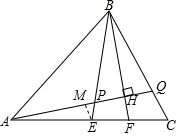 解:作EM∥QC交AQ于M,
解:作EM∥QC交AQ于M,
∵E是AC中点,
∴EM=$\frac{1}{2}$CQ,且∠EMH=∠BQH,
∵BF平分∠EBC,BF⊥PQ,
∴△BPQ是等腰三角形,
∴∠BPQ=∠BQP,
∵∠MPE=∠BPQ,
∴∠EMH=∠MPE,
∴EP=EM=$\frac{1}{2}$CQ,
∴$\frac{EP}{CQ}$=$\frac{1}{2}$.
点评 本题考查了平行线分线段成比例定理,三角形的中位线的性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
6. 如图所示,在一块长为22m,宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),若剩余部分种上草坪,使草坪的面积为300m2,则所修道路的宽度为( )m.
如图所示,在一块长为22m,宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),若剩余部分种上草坪,使草坪的面积为300m2,则所修道路的宽度为( )m.
 如图所示,在一块长为22m,宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),若剩余部分种上草坪,使草坪的面积为300m2,则所修道路的宽度为( )m.
如图所示,在一块长为22m,宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),若剩余部分种上草坪,使草坪的面积为300m2,则所修道路的宽度为( )m.| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
4.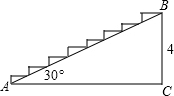 现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)
现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)
 现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)
现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)| A. | 6.9m | B. | 4m | C. | 8m | D. | 10.9m |
 为测量塔的高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是45°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是40m,根据以上观测数据,求观光塔CD的高度.
为测量塔的高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是45°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是40m,根据以上观测数据,求观光塔CD的高度. 如图,在四边形ABCD中,∠D=90°,AB=12,CD=3,DA=4,BC=13,求S四边形ABCD.
如图,在四边形ABCD中,∠D=90°,AB=12,CD=3,DA=4,BC=13,求S四边形ABCD.


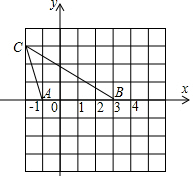 △ABC在平面直角坐标系中的位置如图所示,现另有一点D,满足以A,B,D为顶点的三角形与△ABC全等,则D点坐标为(4,3)或(-2,-3)或(4,-3).
△ABC在平面直角坐标系中的位置如图所示,现另有一点D,满足以A,B,D为顶点的三角形与△ABC全等,则D点坐标为(4,3)或(-2,-3)或(4,-3). 如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{FC}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{FC}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.