为测量塔的高度.如图.一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是45°.然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°．已知楼房高AB约是40m.根据以上观测数据.求观光塔CD的高度．题目和参考答案——青夏教育精英家教网—

题目内容

1．

为测量塔的高度，如图，一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是45°，然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°．已知楼房高AB约是40m，根据以上观测数据，求观光塔CD的高度．

分析根据正切的定义求出AD，根据等腰直角三角形的性质解答即可．

解答解：由题意得：∠BDA=30°，∠CAD=45°，AB=40，
在Rt△ABD中，tan∠ADB=$\frac{AB}{AD}$，
则AD=$\frac{AB}{tan∠ADB}$=40$\sqrt{3}$，
CD=AD=40$\sqrt{3}$，
答：观光塔CD高为40$\sqrt{3}$m．

点评本题考查的是解直角三角形的应用-仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．

练习册系列答案

相关题目

11．

如图，用方向和距离表示火车站相对于仓库的位置是东偏北20°方向，距离仓库50km．

12．

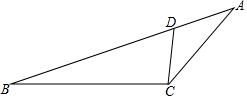如图，点D在△ABC的AB边上，且∠ACD=∠A．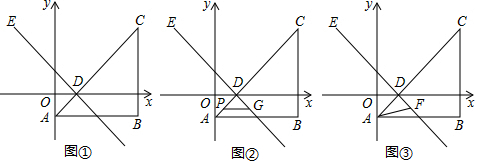
（1）作∠CDE=∠ACD，交BC于点E（尺规作图，保留作图痕迹，不要求写作法）；
（2）在（1）的条件下，判断∠CDE与∠BDE的数量关系，并说明理由．

9．如图①，等腰直角三角形ABC的顶点A的坐标为（0，-1），C的坐标为（4，3），直角顶点B在第四象限，线段AC与x轴交于点D．将线段DC绕点D逆时针旋转90°至DE．

（1）直接写出点B、D、E的坐标并求出直线DE的解析式．
（2）如图②，点P以每秒1个单位的速度沿线段AC从点A运动到点C的过程中，过点P作与x轴平行的直线PG，交直线DE于点G，求与△DPG的面积S与运动时间t的函数关系式，并求出自变量t的取值范围．
（3）如图③，设点F为直线DE上的点，连接AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FE以每秒$\sqrt{2}$个单位的速度运动到E后停止．当点F的坐标是多少时，是否存在点M在整个运动过程中用时最少？若存在，请求出点F的坐标；若不存在，请说明理由．

16．若反比例函数y=$\frac{k}{x}$图象经过点（-1，6），则k=-6．

6．

如图，四边形ABCD中，∠A=90°，AB=2$\sqrt{5}$，AD=2，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别是DM，MN的中点，则EF长度的最大值为$\sqrt{6}$．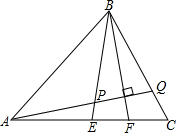

13．多项式2+4x²y-$\frac{1}{3}$x²y³是2，4x²y，-$\frac{1}{3}$x²y³三项的和，其中次数最高项的系数是-$\frac{1}{3}$．

10．二次函数y=ax²-2ax+a-2的图象与y轴交于点C，与x轴交于点A、B两点，O为坐标原点，若OC²=OA•OB，则a=1或1+$\sqrt{2}$．

14．

如图，△ABC中，BE为AC边的中线，BF平分∠EBC，AQ⊥BF交BE于P，交BC于Q，求$\frac{EP}{CQ}$．

试题分类