题目内容
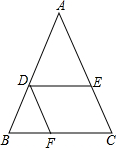如图，在△ABC中，D、E、F分别为AB、AC、BC上的点，且DE∥BC、DF∥AC，若BF=3，CF=2，DF=6，你能求出线段AE的长度吗？考点：相似三角形的判定与性质
专题：
分析：首先证明四边形DFCE为平行四边形，△BDF∽△BAC，得到CE=DF=6，
=
，根据已知条件问题即可解决．
| BF |
| BC |
| DF |
| AC |
解答：解：∵DE∥BC、DF∥AC，
∴四边形DFCE为平行四边形，△BDF∽△BAC，
∴CE=DF=6，
=
；
而BF=3，BC=5，DF=6，
∴AC=10，AE=10-6=4．
解：∵DE∥BC、DF∥AC，∴四边形DFCE为平行四边形，△BDF∽△BAC，
∴CE=DF=6，
| BF |
| BC |
| DF |
| AC |
而BF=3，BC=5，DF=6，
∴AC=10，AE=10-6=4．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是准确找出命题中隐含的等量关系，深入分析，合理推断，科学论证．
练习册系列答案
相关题目
如图所示，已知：BD=DC，求证：EA•FB=EC•FA．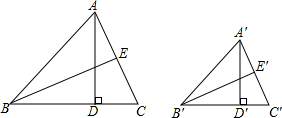
如图，已知△ABC∽△A′B′C′，AD，BE分别是△ABC的高和中线，A′D′，B′E′分别是△A′B′C′的高和中线，求证：AD•B′E′=BE•A′D′．
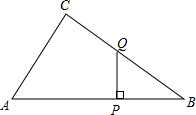如图所示，在Rt△ABC中，∠ACB=90°，P为AB边上一点，Q为BC边上一点．PQ⊥AB，垂足为P，且△BPQ的面积等于四边形APQC面积的