题目内容
计算:1002-992+982-972+…+22-1= .
考点:因式分解-运用公式法
专题:
分析:把所求的式子的第一项与最后一项结合,第二项与倒数第二项结合,依次结合了50组,把结合后的偶次项提取-1,然后分别运用平方差公式变形,提取101后得到25个2相加,从而计算出结果.
解答:解:1002-992+982-972+…+22-12
=(1002-12)-(992-22)+(982-32)-…+(522-492)-(512-502)
=(100+1)(100-1)-(99+2)(99-2)+(98+3)(98-3)-…+(52+49)(52-49)-(51+50)(51-50)
=101×99-101×97+101×95-…+101×3-101×1
=101×(99-97+95-…+3-1)
=101×(2+2+…+2)
=101×25×2
=5050.
故答案为:5050.
=(1002-12)-(992-22)+(982-32)-…+(522-492)-(512-502)
=(100+1)(100-1)-(99+2)(99-2)+(98+3)(98-3)-…+(52+49)(52-49)-(51+50)(51-50)
=101×99-101×97+101×95-…+101×3-101×1
=101×(99-97+95-…+3-1)
=101×(2+2+…+2)
=101×25×2
=5050.
故答案为:5050.
点评:此题考查了平方差公式的运用,技巧性比较强,要求学生多观察式子的特点,注意结合的方法,找到第一项与最后一项结合,第二项与倒数第二项结合,依此类推的结合方法是解本题的关键.

练习册系列答案
相关题目
用配方法解方程x2-6x-1=0,经过配方,得到( )
| A、(x+3)2=10 |
| B、(x-3)2=1 |
| C、(x-3)2=4 |
| D、(x-3)2=10 |
x与y的平方差,用代数式表示正确的是( )
| A、(x-y)2 |
| B、x-y2 |
| C、x2-y |
| D、x2-y2 |
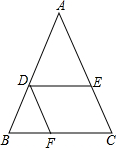 如图,在△ABC中,D、E、F分别为AB、AC、BC上的点,且DE∥BC、DF∥AC,若BF=3,CF=2,DF=6,你能求出线段AE的长度吗?
如图,在△ABC中,D、E、F分别为AB、AC、BC上的点,且DE∥BC、DF∥AC,若BF=3,CF=2,DF=6,你能求出线段AE的长度吗?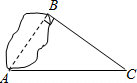 如图,为测得到池塘两岸点A和点B间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长20米、BC长16米,则A、B两点间距离是
如图,为测得到池塘两岸点A和点B间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长20米、BC长16米,则A、B两点间距离是