题目内容
如图所示，已知：BD=DC，求证：EA•FB=EC•FA．考点：相似三角形的判定与性质
专题：证明题
分析：过过A作AM∥BC交DF于M，利用平行线分线段成比例可得到有
=
，
=
，结合条件，再把比例化为乘积即可得到结论．
| AM |
| BD |
| FA |
| FB |
| AM |
| DC |
| AE |
| EC |
解答：
证明：
过A作AM∥BC交DF于M，则有
=
，
=
，
∵BD=DC，
∴
=
，
∴EA•FB=EC•FA．
证明：过A作AM∥BC交DF于M，则有
| AM |
| BD |
| FA |
| FB |
| AM |
| DC |
| AE |
| EC |
∵BD=DC，
∴
| FA |
| FB |
| AE |
| EC |
∴EA•FB=EC•FA．
点评：本题主要考查平行线分线段成比例的性质，作出平行线得到线段的比例关系是解题的关键．
练习册系列答案
相关题目
x与y的平方差，用代数式表示正确的是（ ）
| A、（x-y）2 |
| B、x-y2 |
| C、x2-y |
| D、x2-y2 |
如图，已知EF⊥FD，AB⊥FD，CD⊥FD，EF=1.5，AB=2.5，FB=2.2，BD=3.6，求CD的长．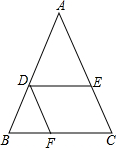
如图，在△ABC中，D、E、F分别为AB、AC、BC上的点，且DE∥BC、DF∥AC，若BF=3，CF=2，DF=6，你能求出线段AE的长度吗？
如图，在△ABC中，点D、E分别在AB、AC上，DE∥BC，下列比例式中，不正确的是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|