题目内容
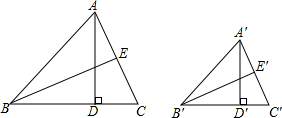 如图,已知△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,A′D′,B′E′分别是△A′B′C′的高和中线,求证:AD•B′E′=BE•A′D′.
如图,已知△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,A′D′,B′E′分别是△A′B′C′的高和中线,求证:AD•B′E′=BE•A′D′.考点:相似三角形的判定与性质
专题:证明题
分析:直接运用相似三角形的性质,列出比例式
=
,
=
,经比较得到
=
,即可解决问题.
| AD |
| A′D′ |
| BC |
| B′C′ |
| BE |
| B′E′ |
| BC |
| B′C′ |
| AD |
| A′D′ |
| BE |
| B′E′ |
解答: 证明:∵△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,
证明:∵△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,
且A′D′,B′E′分别是△A′B′C′的高和中线,
∴
=
,
=
,
∴
=
,
∴AD•B′E′=BE•A′D′.
 证明:∵△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,
证明:∵△ABC∽△A′B′C′,AD,BE分别是△ABC的高和中线,且A′D′,B′E′分别是△A′B′C′的高和中线,
∴
| AD |
| A′D′ |
| BC |
| B′C′ |
| BE |
| B′E′ |
| BC |
| B′C′ |
∴
| AD |
| A′D′ |
| BE |
| B′E′ |
∴AD•B′E′=BE•A′D′.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入分析,合理推断、大胆猜想、科学论证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列黑体英文大写字母中形状上与其余三个不同的是( )
| A、E | B、M | C、N | D、H |
抛物线y=-(a+8)2+2的顶点坐标是( )
| A、(-8,2) |
| B、(8,2) |
| C、(2,8) |
| D、(-8,-2) |
有1角、5角、1元三种硬币15枚,共7元,则这三种硬币各有( )
| A、3枚、7枚、5枚 |
| B、5枚、7枚、3枚 |
| C、7枚、5枚、3枚 |
| D、3枚、5枚、7枚 |
 如图,AD∥EG∥BC,AD=6,BC=9,AE:AB=2:3,求GF的长.
如图,AD∥EG∥BC,AD=6,BC=9,AE:AB=2:3,求GF的长.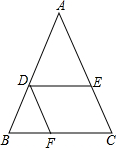 如图,在△ABC中,D、E、F分别为AB、AC、BC上的点,且DE∥BC、DF∥AC,若BF=3,CF=2,DF=6,你能求出线段AE的长度吗?
如图,在△ABC中,D、E、F分别为AB、AC、BC上的点,且DE∥BC、DF∥AC,若BF=3,CF=2,DF=6,你能求出线段AE的长度吗?