题目内容
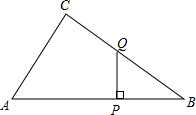 如图所示,在Rt△ABC中,∠ACB=90°,P为AB边上一点,Q为BC边上一点.PQ⊥AB,垂足为P,且△BPQ的面积等于四边形APQC面积的
如图所示,在Rt△ABC中,∠ACB=90°,P为AB边上一点,Q为BC边上一点.PQ⊥AB,垂足为P,且△BPQ的面积等于四边形APQC面积的| 1 |
| 4 |
考点:相似三角形的判定与性质,勾股定理
专题:
分析:由条件可证得△BPQ∽△BCA,又由面积关系可求得其相似比为
=
,可求得BQ,在Rt△BPQ中利用勾股定理可求得PQ.
| BQ |
| BA |
| 1 | ||
|
解答:解:∵△BPQ的面积等于四边形APQC面积的
,
∴
=
,
∵PQ⊥AB,
∴∠BPQ=∠ACB,
∴△BPQ∽△BCA,
∴
=
=
,
且BA=5cm,
∴
=
,
∴BQ=
cm,
在Rt△BPQ中,BP=2cm,
∴PQ=1cm.
| 1 |
| 4 |
∴
| S△BPQ |
| S△BCA |
| 1 |
| 5 |
∵PQ⊥AB,
∴∠BPQ=∠ACB,
∴△BPQ∽△BCA,
∴
| BQ |
| BA |
|
| 1 | ||
|
且BA=5cm,
∴
| BQ |
| 5 |
| 1 | ||
|
∴BQ=
| 5 |
在Rt△BPQ中,BP=2cm,
∴PQ=1cm.
点评:本题主要考查相似三角形的判定和性质,利用面积关系求得相似比是解题的关键,注意勾股定理的运用.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,下列比例式中,不正确的是( )
如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,下列比例式中,不正确的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
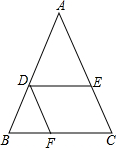 如图,在△ABC中,D、E、F分别为AB、AC、BC上的点,且DE∥BC、DF∥AC,若BF=3,CF=2,DF=6,你能求出线段AE的长度吗?
如图,在△ABC中,D、E、F分别为AB、AC、BC上的点,且DE∥BC、DF∥AC,若BF=3,CF=2,DF=6,你能求出线段AE的长度吗?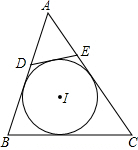 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为( )
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为( )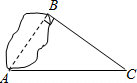 如图,为测得到池塘两岸点A和点B间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长20米、BC长16米,则A、B两点间距离是
如图,为测得到池塘两岸点A和点B间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长20米、BC长16米,则A、B两点间距离是