题目内容
若x+y=m,xy=n,则(x-y)2= ,x2+y2= .
考点:完全平方公式
专题:
分析:先根据完全平方公式变形得到(x-y)2=(x+y)2-4xy,x2+y2=(x+y)2-2xy,分别把x+y=m,xy=n整体代入计算即可.
解答:解:∵x+y=m,xy=n,
∴(x-y)2=(x+y)2-4xy=m2-4n;
x2+y2=(x+y)2-2xy=m2-2n.
故答案为:m2-4n,m2-2n.
∴(x-y)2=(x+y)2-4xy=m2-4n;
x2+y2=(x+y)2-2xy=m2-2n.
故答案为:m2-4n,m2-2n.
点评:本题考查了完全平方公式:完全平方公式:(a±b)2=a2±2ab+b2.也考查了代数式的变形能力.

练习册系列答案
相关题目
抛物线y=-(a+8)2+2的顶点坐标是( )
| A、(-8,2) |
| B、(8,2) |
| C、(2,8) |
| D、(-8,-2) |
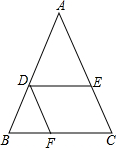 如图,在△ABC中,D、E、F分别为AB、AC、BC上的点,且DE∥BC、DF∥AC,若BF=3,CF=2,DF=6,你能求出线段AE的长度吗?
如图,在△ABC中,D、E、F分别为AB、AC、BC上的点,且DE∥BC、DF∥AC,若BF=3,CF=2,DF=6,你能求出线段AE的长度吗? 如图,为测得到池塘两岸点A和点B间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长20米、BC长16米,则A、B两点间距离是
如图,为测得到池塘两岸点A和点B间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长20米、BC长16米,则A、B两点间距离是