题目内容
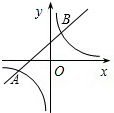 如图,已知一次函数与反比例函数的图象交于点A(-3,-1)和B(a,3).
如图,已知一次函数与反比例函数的图象交于点A(-3,-1)和B(a,3).(1)求反比例函数的解析式和点B的坐标;
(2)连结AO和BO,判断△ABO的形状,请说明理由,并求出它的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)设反比例函数的解析式是y=
,将A(-3,-1)代入求出k,即可得出反比例函数的解析式,把B的坐标代入求出即可;
(2)求出一次函数的解析式,求出一次函数和y轴的交点坐标,根据三角形的面积公式求出即可.
| k |
| x |
(2)求出一次函数的解析式,求出一次函数和y轴的交点坐标,根据三角形的面积公式求出即可.
解答:解:(1)设反比例函数的解析式是y=
,
将A(-3,-1)代入,求得k=3,
所以反比例函数的解析式是:y=
,
将B(a,3)代入,求得a=1,
所以B的坐标是(1,3);
(2)△AOB是等腰三角形,
理由是:∵A(-3,-1)和B(1,3),
∴由勾股定理得:AO=BO=
,
∴△AOB是等腰三角形,
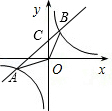 设一次函数的解析式是y=ax+c,
设一次函数的解析式是y=ax+c,
把A、B的坐标代入得:
,
解得:a=1,c=2,
所以一次函数的解析式是y=x+2,
当x=0时,y=2,
即OC=2,
所以△AOB的面积S=S△AOC+S△BOC=
×2×3+
×2×1=4.
| k |
| x |
将A(-3,-1)代入,求得k=3,
所以反比例函数的解析式是:y=
| 3 |
| x |
将B(a,3)代入,求得a=1,
所以B的坐标是(1,3);
(2)△AOB是等腰三角形,
理由是:∵A(-3,-1)和B(1,3),
∴由勾股定理得:AO=BO=
| 10 |
∴△AOB是等腰三角形,
 设一次函数的解析式是y=ax+c,
设一次函数的解析式是y=ax+c,把A、B的坐标代入得:
|
解得:a=1,c=2,
所以一次函数的解析式是y=x+2,
当x=0时,y=2,
即OC=2,
所以△AOB的面积S=S△AOC+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了一次函数与反比例函数的交点问题,用待定系数法求出函数的解析式,三角形的面积的应用,主要考查学生的理解能力和计算能力,题目比较典型,难度适中.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
2014年3月份,萧山市区一周空气质量报告中某项污染指数的数据是:61,75,61,63,50,63,61,则下列表述错误的是( )
| A、中位数是62 |
| B、众数是61 |
| C、平均数是62 |
| D、极差是25 |

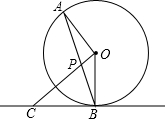 如图,AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC.
如图,AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC.