题目内容
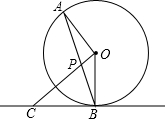 如图,AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC.
如图,AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC.(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若tan∠A=
| 1 |
| 3 |
考点:切线的判定,勾股定理
专题:
分析:(1)根据等腰三角形的性质求得∠OBP+∠CBP=90°,则BC是⊙O的切线;
(2)根据锐角三角函数定义,可设OP=x,则OA=3x.在Rt△OBC中,由勾股定理列出关于x的方程(x+8)2=(3x)2+82,通过解该方程可以求得x=2,则OA=3x=6.
(2)根据锐角三角函数定义,可设OP=x,则OA=3x.在Rt△OBC中,由勾股定理列出关于x的方程(x+8)2=(3x)2+82,通过解该方程可以求得x=2,则OA=3x=6.
解答:解:(1)相切.理由如下:
∵OA=OB,
∴∠A=∠OBA.
∵CP=BP,
∴∠CBP=∠BPC.
∵∠OPA=∠BPC,∠A+∠OPA=90°,
∴∠OBP+∠CBP=90°,
∴BC是⊙O的切线;
(2)∵tanA=
=
,
∴设OP=x,则OA=3x.
在Rt△OBC中,(x+8)2=(3x)2+82,
解得 x=2,则OA=6,
∴⊙O的半径是6.
∵OA=OB,
∴∠A=∠OBA.

∵CP=BP,
∴∠CBP=∠BPC.
∵∠OPA=∠BPC,∠A+∠OPA=90°,
∴∠OBP+∠CBP=90°,
∴BC是⊙O的切线;
(2)∵tanA=
| OP |
| OA |
| 1 |
| 3 |
∴设OP=x,则OA=3x.
在Rt△OBC中,(x+8)2=(3x)2+82,
解得 x=2,则OA=6,
∴⊙O的半径是6.
点评:本题综合考查了圆的切线,勾股定理,等腰三角形的性质等知识点的运用,知道圆的切线,连接圆心和切点,题目综合性比较强,通过做此题培养了学生综合运用定理进行推理和计算的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
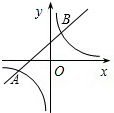 如图,已知一次函数与反比例函数的图象交于点A(-3,-1)和B(a,3).
如图,已知一次函数与反比例函数的图象交于点A(-3,-1)和B(a,3).