题目内容
11.如果一个正整数能表示为两个连续偶数的平方差,那么我们称这个正整数为“和谐数”,如4=22-02,12=42-22,20=62-42,因此,4,12,20这三个数都是“和谐数”.(1)当28=m2-n2时,m+n=14;
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构成的“和谐数”是4的倍数吗?为什么?
分析 (1)利用“和谐数”的定义得到m-n=2,已知等式右边利用平方差公式化简,即可确定出m+n的值;
(2)表示出两个连续偶数的平方差,整理后即可作出判断.
解答 解:(1)∵28=m2-n2=(m+n)(m-n),且m-n=2,
∴m+n=14;
故答案为:14;
(2)(2k+2)2-(2k)2=(2k+2+2k)(2k+2-2k)=2(4k+2)=4(2k+1),
∵k为非负整数,
∴2k+1一定为正整数,
∴4(2k+1)一定能被4整除,
则由这两个连续偶数构成的“和谐数”是4的倍数.
点评 此题考查了平方差公式,以及规律型:数字的变化类,弄清题中“和谐数”的定义是解本题的关键.

练习册系列答案
相关题目
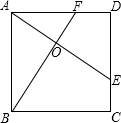 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AO=OE (2)S△AOB=S四边形DEOF (3)AE=BF (4)AE⊥BF中,正确的有(2)、(3)、(4)..
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AO=OE (2)S△AOB=S四边形DEOF (3)AE=BF (4)AE⊥BF中,正确的有(2)、(3)、(4)..
 函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-3=0的根的情况是方程ax2+bx+c-3=0有两个相等的实数根.
函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-3=0的根的情况是方程ax2+bx+c-3=0有两个相等的实数根. 如图,将正方形ABCD的边BC延长到E,使CE=AC,AE与DC交于点F,则CE:FC=$\sqrt{2}$+1.
如图,将正方形ABCD的边BC延长到E,使CE=AC,AE与DC交于点F,则CE:FC=$\sqrt{2}$+1.