题目内容
2．
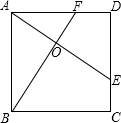如图，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列结论：（1）AO=OE （2）S△AOB=S四边形DEOF （3）AE=BF （4）AE⊥BF中，正确的有（2）、（3）、（4）．．
分析 根据正方形的性质，运用SAS证明△ABF≌△DAE，运用全等三角形性质逐一解答．
解答 解：∵四边形ABCD是正方形，
∴AB=AD，∠BAF=∠ADE=90°．
∵CE=DF，
∴AF=DE．
∴△ABF≌△DAE．
∴AE=BF；
∠AFB=∠AED．
∵∠AED+∠DAE=90°，
∴∠AFB+∠DAE=90°，
∴∠AOF=90°，即AE⊥BF；
S△AOB=S△ABF-S△AOF，S四边形DEOF=S△ADE-S△AOF，
∵△ABF≌△DAE，
∴S△ABF=S△ADE，
∴S△AOB=S四边形DEOF．
故答案为：（2）、（3）、（4）．
点评 此题考查正方形的性质、全等三角形的判定和性质、三角形内角和定理等知识点，有一定的综合性．
练习册系列答案
相关题目
如图，用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD，中间是空的小正方形EFGH．若AB=a，EF=b，判断以下关系式：
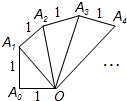如图是由一系列直角三角形组成的螺旋形，OA=OA1=OA2=…OAn=1，则第n个直角三角形的面积为$\frac{\sqrt{n}}{2}$．
如图，在△ABC中，∠C=90°，AC=12，∠A的平分线AD=8$\sqrt{3}$，则AB=24，BC=12$\sqrt{3}$．